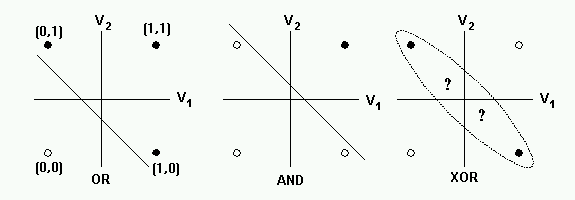Machine Learning with Python

심층 신경망(DEEP NEURAL NETWORK)

• 단순 신경망(입력층과 출력층으로 이루어진 모델)은 AND나 OR, NOT 게이트와 같이 선형적인 분류만 가능

• XOR 게이트와 같이 비선형적인 분류를 하기 위해서는 AND와 OR, NOT 게이트를 조합하면 가능했던 것과 같이 신경망에 은닉층으로 추가하면 비선형 분류를 할 수 있다

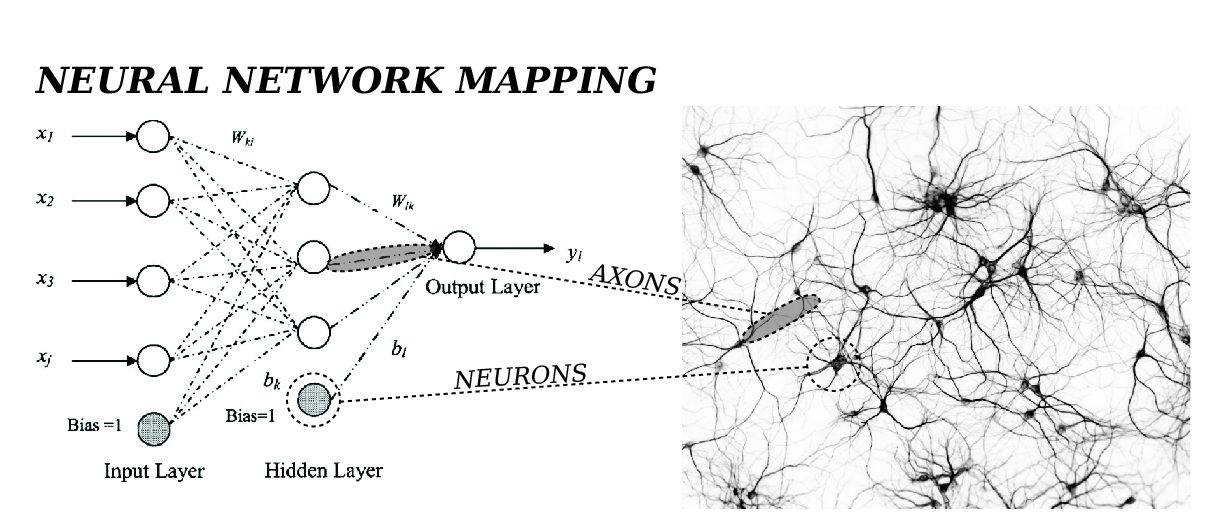
• 신경망 : 각 뉴런의 발화하는 패턴을 조합하여 데이터를 분류하는 것이기 때문에 뉴런의 개수를 늘려 조합하면 더욱 복잡한 패턴을 인식하고 분류할 수 있음

• 뉴런을 늘리는 방법
• 은닉층에서 뉴런의 개수를 늘리기
• 은닉층의 개수를 늘리기

• 은닉층의 개수를 늘리면 신경망의 층을 더 두텁게 만드는데, 이렇게 두터운 층을 이루는 네트워크를 심층 신경망(Deep Neural Network)라고 하며, 심층 신경망을 학습시키는 기법을 딥러닝(Deep Learning) 또는 심층 학습이라고 한다

MNIST 분류

• MNIST(Modified National Institute of Standards of Technology) 데이터
  • TenforFlow
  • 5,5000장 : 학습용 데이터
  • 1,0000장 : 테스트용 데이터
  • 5000장 : 검증용 데이터
  • sklearn 또는 keras
  • 6,0000장 : 학습용 데이터
  • 1,0000장 : 테스트용 데이터
• 7,0000장 이미지 데이터 : 아래 그림과 같이 0에서 9까지의 손글씨 숫자 이미지($28\times 28$ 픽셀)로 각각의 숫자가 레이블(label)임

그림 7.1 MNIST 이미지 데이터

• MNIST 데이터는 sklearn이나 TensorFlow, Keras를 사용해 불러올 수 있다

from sklearn 
import datasets 

MNIST_sklearn = datasets.fetch_mldata('MNIST original', data_home='.') 
X = MNIST_sklearn.data 
Y = MNIST_sklearn.target 


from tensorflow.examples.tutorials.mnist import input_data 

MNIST_TensorFlow = input_data.read_data_sets("../MNIST_data/", one_hot=True) 

X_train = MNIST_TensorFlow.train.images 
Y_train = MNIST_TensorFlow.train.labels 

X_test = MNIST_TensorFlow.test.images 
Y_test = MNIST_TensorFlow.test.labels 

X_validation = MNIST_TensorFlow.validation.images 
Y_validation = MNIST_TensorFlow.validation.labels 

from keras.datasets import mnist 
(X_train, Y_train), (X_test, Y_test) = mnist.load_data()

• MNIST 분류 학습 코드
• 학습 데이터와 테스트 데이터를 합쳐서 1,0000개의 데이터만 사용
• 입력층 차원 : $783(=28\times 28)$
• 은닉층 차원 : $200$개의 뉴런을 사용

import numpy as np 
from keras.models 
import Sequential 
from keras.layers 
import Dense, Activation from keras.optimizers 
import SGD 
from sklearn import datasets 
from sklearn.model_selection import train_test_split 

MNIST = datasets.fetch_mldata('MNIST original', data_home='.') 
n = len(MNIST.data) 
N = 10000 
indices = np.random.permutation(range(n))[:N] 

X = MNIST.data[indices] 
Y = MNIST.target[indices] 

Y = np.eye(10)[Y.astype(int)] 
x_train, x_test, y_train, y_test = train_test_split(X, Y, train_size=0.8) # 모델 설정 
n_in = len(X[0]) 
n_hidden = 200 
n_out = len(Y[0]) 

model = Sequential() 
model.add(Dense(input_dim=n_in, units=n_hidden)) 
model.add(Activation('sigmoid')) 
model.add(Dense(units=n_out)) 
model.add(Activation('softmax')) 
model.compile(loss='categorical_crossentropy', optimizer=SGD(lr=0.1), metrics=['accuracy']) 

print(f'\nWhen neurons are , Elapse training time : seconds') # 정확도 측정 

start = time() 
loss_and_metrics = model.evaluate(x_test, y_test) 

print(f'\nLoss : ') print(f'Accuracy : %') 
print(f'When neurons are , Elapse test time : seconds')

은닉층 뉴런의 개수에 따른 정확도 비교

• 뉴런 200개일 때

When neurons are 200, Elapse training time : 161.34555006027222 seconds 

  32/2000 [..............................] - ETA: 0s 
2000/2000 [==============================] - 0s 23us/step 

Loss : 0.315761 Accuracy : 91.3% 

When neurons are 200, Elapse test time : 0.046033620834350586 seconds

• 뉴런 400개일 때

When neurons are 400, Elapse training time : 338.7665045261383 seconds 

  32/2000 [..............................] - ETA: 0s 
1408/2000 [====================>.........] - ETA: 0s 
2000/2000 [==============================] - 0s 45us/step 

Loss : 0.255655 Accuracy : 92.5% 

When neurons are 400, Elapse test time : 0.09006357192993164 seconds

• 뉴런 800개 일 때

When neurons are 800, Elapse training time : 588.1928327083588 seconds 

  32/2000 [..............................] - ETA: 0s 
1248/2000 [=================>............] - ETA: 0s 
2000/2000 [==============================] - 0s 49us/step 

Loss : 0.282248 Accuracy : 92.6% 

When neurons are 800, Elapse test time : 0.09756922721862793 seconds

• 뉴런 1000개일 때

When neurons are 1000, Elapse training time : 737.0927028656006 seconds 
  32/2000 [..............................] - ETA: 0s 
 992/2000 [=============>................] - ETA: 0s 
1920/2000 [===========================>..] - ETA: 0s 
2000/2000 [==============================] - 0s 59us/step 

Loss : 1.66926 Accuracy : 84.8% 

When neurons are 1000, Elapse test time : 0.11908316612243652 seconds

• 뉴런 2000개일 때

When neurons are 2000, Elapse training time : 1447.6608402729034 seconds 

  32/2000 [..............................] - ETA: 0s 
 576/2000 [=======>......................] - ETA: 0s 
1056/2000 [==============>...............] - ETA: 0s 
1568/2000 [======================>.......] - ETA: 0s 
2000/2000 [==============================] - 0s 105us/step 

Loss : 1.61429 Accuracy : 87.55% 

When neurons are 2000, Elapse test time : 0.21014928817749023 seconds

• 뉴런 4000개일 때

When neurons are 4000, Elapse training time : 2890.275902748108 seconds  
  32/2000 [..............................] - ETA: 1s 
 288/2000 [===>..........................] - ETA: 0s 
 544/2000 [=======>......................] - ETA: 0s 
 800/2000 [===========>..................] - ETA: 0s 
1056/2000 [==============>...............] - ETA: 0s 
1312/2000 [==================>...........] - ETA: 0s 
1568/2000 [======================>.......] - ETA: 0s 
1824/2000 [==========================>...] - ETA: 0s 
2000/2000 [==============================] - 0s 217us/step 

Loss : 9.80855 Accuracy : 37.95% 

When neurons are 4000, Elapse test time : 0.4558277130126953 seconds

• 뉴런 1,0000개일 때

When neurons are 10000, Elapse training time : 6894.483572006226 seconds

  32/2000 [..............................] - ETA: 2s
 160/2000 [=>............................] - ETA: 0s
 288/2000 [===>..........................] - ETA: 0s
 416/2000 [=====>........................] - ETA: 0s
 544/2000 [=======>......................] - ETA: 0s
 672/2000 [=========>....................] - ETA: 0s
 832/2000 [===========>..................] - ETA: 0s
 960/2000 [=============>................] - ETA: 0s
1088/2000 [===============>..............] - ETA: 0s
1216/2000 [=================>............] - ETA: 0s 
1344/2000 [===================>..........] - ETA: 0s
1472/2000 [=====================>........] - ETA: 0s 
1600/2000 [=======================>......] - ETA: 0s 
1728/2000 [========================>.....] - ETA: 0s 
1856/2000 [==========================>...] - ETA: 0s 
2000/2000 [==============================] - 1s 414us/step 

Loss : 12.5196 Accuracy : 22.1% 

When neurons are 10000, Elapse test time : 0.8445994853973389 seconds

• 은닉층 뉴런의 수와 정확도, 학습시간 등의 비교

표 7.1  1개의 은닉층에 있는 뉴런의 개수에 따른 성능 비교

그림 7.2 1개의 은닉층에 있는 뉴런의 개수에 따른 성능 비교

• 표 7.1과 그림 7.2를 보면 은닉층의 뉴런의 개수를 늘리더라도 신경망 모델의 예측 정확도가 높아지다가 떨어지는 것을 알 수 있다. 즉, 뉴런의 개수를 단순히 늘린다고 정확도가 높아진다고 볼 수가 없다

• 또한 뉴런의 개수를 늘리면 학습에 걸리는 시간 또한 무시할 수 없을 정도로 길어지는 것을 알 수 있다

• 각 층의 뉴런의 개수를 $n_i, n_h, n_o$로 나타낸다면 각각의 뉴런이 연결되는 가지의 수는 $n_i\times n_h + n_h\times n_o$이기 때문에 모델의 예측 정확도가 동일하다면 은닉층 뉴런의 개수 $n_h$가 작을 수록 좋다

은닉층 뉴런의 개수가 일정할 때 은닉층의 개수에 따른 정확도 비교

• Keras에서 은닉층의 개수를 추가하는 것은 간단하다

from time import time 
import numpy as np 
from keras.models import Sequential 
from keras.layers import Dense, Activation 
from keras.optimizers import SGD 
from sklearn import datasets 
from sklearn.model_selection import train_test_split 

start = time() 
MNIST = datasets.fetch_mldata('MNIST original', data_home='.') 

n = len(MNIST.data) 
N = 10000 

indices = np.random.permutation(range(n))[:N] 

X = MNIST.data[indices] 
Y = MNIST.target[indices] 
Y = np.eye(10)[Y.astype(int)] 
x_train, x_test, y_train, y_test = train_test_split(X, Y, train_size=0.8) # 모델 설정 

n_in = len(X[0]) 
n_hidden = 200 
n_out = len(Y[0]) 
model = Sequential() 
model.add(Dense(input_dim=n_in, units=n_hidden)) 
model.add(Activation('sigmoid')) # 은닉층 1개 추가 
model.add(Dense(units=n_hidden)) 
model.add(Activation('sigmoid')) 
model.add(Dense(units=n_out)) 
model.add(Activation('softmax')) 
model.compile(loss='categorical_crossentropy', optimizer=SGD(lr=0.1), metrics=['accuracy']) # 모델 학습 

epochs = 1000 
batch_size = 100 

model.fit(x_train, y_train, epochs=epochs, batch_size=batch_size) 

print(f'\nWhen hidden layers are 2, Elapse training time : seconds\n') # 정확도 측정 

start = time() 
loss_and_metrics = model.evaluate(x_test, y_test) 

print(f'\nLoss : ') 
print(f'Accuracy : %') 
print(f'When hidden layers are 2, Elapse test time : seconds')

• 은닉층의 개수가 2개일 때

When hidden layers are 2, Elapse training time : 221.6898009777069 seconds

  32/2000 [..............................] - ETA: 0s 
2000/2000 [==============================] - 0s 26us/step 

Loss : 0.314476 Accuracy : 91.1% 

When hidden layers are 2, Elapse test time : 0.05203652381896973 seconds

• 은닉층의 개수가 3개일 때

When hidden layers are 3, Elapse training time : 4.0분 31.61421251296997초 

  32/2000 [..............................] - ETA: 1s 
1408/2000 [====================>.........] - ETA: 0s 
2000/2000 [==============================] - 0s 46us/step 

Loss : 0.327307 Accuracy : 90.85%

When hidden layers are 3, Elapse test time : 0.0분 0.09306979179382324초

• 은닉층의 개수가 4개일 때

When hidden layers are 4, Elapse training time : 5.0분 7.0608086585998535초

  32/2000 [..............................] - ETA: 0s 
1920/2000 [===========================>..] - ETA: 0s 
2000/2000 [==============================] - 0s 33us/step 

Loss : 0.384374 Accuracy : 88.8% 

When hidden layers are 4, Elapse test time : 0.0분 0.06604671478271484초 acy

• 은닉층의 개수가 5개일 때

When hidden layers are 5, Elapse training time : 5.0분 32.52758073806763초 

  32/2000 [..............................] - ETA: 0s 
1856/2000 [==========================>...] - ETA: 0s 
2000/2000 [==============================] - 0s 35us/step 

Loss : 0.43979 Accuracy : 87.55% 

When hidden layers are 5, Elapse test time : 0.0분 0.0695500373840332초

• 은닉층의 개수가 6개일 때

When hidden layers are 6, Elapse training time : 6.0분 29.71598792076111초 

  32/2000 [..............................] - ETA: 1s 
1568/2000 [======================>.......] - ETA: 0s 
2000/2000 [==============================] - 0s 43us/step 

Loss : 0.454472 Accuracy : 86.25% 

When hidden layers are 6, Elapse test time : 0.0분 0.0860595703125초

• 은닉층의 개수가 7개일 때

When hidden layers are 7, Elapse training time : 6.0분 53.46243381500244초 

  32/2000 [..............................] - ETA: 1s 
1472/2000 [=====================>........] - ETA: 0s 
2000/2000 [==============================] - 0s 44us/step

Loss : 0.90537 Accuracy : 70.2% 

When hidden layers are 7, Elapse test time : 0.0분 0.08705806732177734초 

• 은닉층의 개수가 8개일 때

When hidden layers are 8, Elapse training time : 7.0분 55.60267639160156초 

  32/2000 [..............................] - ETA: 1s 
1312/2000 [==================>...........] - ETA: 0s 
2000/2000 [==============================] - 0s 49us/step 

Loss : 2.29931 Accuracy : 12.4% 

When hidden layers are 8, Elapse test time : 0.0분 0.09706592559814453초

• 은닉층의 개수가 9개일 때

When hidden layers are 9, Elapse training time : 8.0분 43.596526861190796초 

32/2000 [..............................] - ETA: 1s 
1152/2000 [================>.............] - ETA: 0s 
2000/2000 [==============================] - 0s 55us/step 

Loss : 2.30193 Accuracy : 9.95% 

When hidden layers are 9, Elapse test time : 0.0분 0.11157894134521484초

• 은닉층의 개수가 10개일 때

When hidden layers are 10, Elapse training time : 9.0분 0.5422961711883545초 

  32/2000 [..............................] - ETA: 1s 
  1216/2000 [=================>............] - ETA: 0s 
  2000/2000 [==============================] - 0s 50us/step 
  
  Loss : 2.30177 Accuracy : 10.05% 
  
  When hidden layers are 10, Elapse test time : 0.0분 0.10107207298278809초

• 은닉층의 개수가 50개일 때

When hidden layers are 50, Elapse training time : 37.0분 29.942996501922607초 

  32/2000 [..............................] - ETA: 6s 
 288/2000 [===>..........................] - ETA: 0s 
 544/2000 [=======>......................] - ETA: 0s 
 832/2000 [===========>..................] - ETA: 0s 
1120/2000 [===============>..............] - ETA: 0s 
1408/2000 [====================>.........] - ETA: 0s 
1696/2000 [========================>.....] - ETA: 0s 
1984/2000 [============================>.] - ETA: 0s 
2000/2000 [==============================] - 0s 245us/step 

Loss : 2.30093 Accuracy : 12.5% 

When hidden layers are 50, Elapse test time : 0.0분 0.5073604583740234초

표 7.2  200개의 뉴런을 가진 은닉층의 개수에 따른 성능 비교

• 표 7.2의 결과는 표 7.1처럼 뉴런의 개수랑 은닉층의 개수를 무작정 늘린다고 예측 결과의 정확도가 높아지지는 않고 오히려 더 떨어지는 결과를 보여준다. 특히 은닉층이 8개인 경우에는 거의 학습이 되지 않았다는 것을 알 수 있다.

PyTorch 코드

• 학습을 위한 코드

import torch
import torchvision.datasets as dsets
import torchvision.transforms as transforms
from torch.utils.data import DataLoader
import torch.nn as nn
import matplotlib.pyplot as plt
import random
from time import time

USE_CUDA = torch.cuda.is_available() # GPU를 사용가능하면 True, 아니라면 False를 리턴
device = torch.device("cuda" if USE_CUDA else "cpu") # GPU 사용 가능하면 사용하고 아니면 CPU 사용
print("다음 기기로 학습합니다:", device)

# for reproducibility
random.seed(777)
torch.manual_seed(777)
if device == 'cuda':
    torch.cuda.manual_seed_all(777)
    
# MNIST dataset
mnist_train = dsets.MNIST(root='MNIST_data/',
                          train=True,
                          transform=transforms.ToTensor(),
                          download=True)

mnist_test = dsets.MNIST(root='MNIST_data/',
                         train=False,
                         transform=transforms.ToTensor(),
                         download=True)
                         
# dataset loader
batch_size = 100
data_loader = DataLoader(dataset=mnist_train,
                         batch_size=batch_size, # 배치 크기는 100
                         shuffle=True,
                         drop_last=True)
                         
# MNIST 데이터 이미지의 크기: 28 * 28 = 784
linear = torch.nn.Linear(784, 10, bias=True).to(device)

# 매개변수
training_epochs = 15
batch_size = 100

# cost/loss 함수와 optimizer 정의
criterion = torch.nn.CrossEntropyLoss().to(device) # 내부적으로 Softmax로 계산됨
optimizer = torch.optim.SGD(linear.parameters(), lr=0.1)

start = time() 

for epoch in range(training_epochs): # 앞서 training_epochs의 값은 15로 지정함.
    avg_cost = 0
    total_batch = len(data_loader)

    for X, Y in data_loader:
        # 배치 크기가 100이므로 아래의 연산에서 X는 (100, 784)의 텐서가 된다.
        X = X.view(-1, 28 * 28).to(device)
        # 레이블은 원-핫 인코딩이 된 상태가 아니라 0 ~ 9의 정수.
        Y = Y.to(device)

        optimizer.zero_grad()
        hypothesis = linear(X)
        cost = criterion(hypothesis, Y)
        cost.backward()
        optimizer.step()

        avg_cost += cost / total_batch

    print(f'Epoch: {epoch + 1:>04d}/{training_epochs:2d}, cost = {avg_cost:>12.9f}')

print(f'Learning finished, Elapse test time : {time() - start:10.4f}seconds')

다음 기기로 학습합니다: cuda

Epoch: 0001/15, cost =  0.534912467
Epoch: 0002/15, cost =  0.359308600
Epoch: 0003/15, cost =  0.331088215
Epoch: 0004/15, cost =  0.316574216
Epoch: 0005/15, cost =  0.307130307
Epoch: 0006/15, cost =  0.300207883
Epoch: 0007/15, cost =  0.294897258
Epoch: 0008/15, cost =  0.290830433
Epoch: 0009/15, cost =  0.287419587
Epoch: 0010/15, cost =  0.284589082
Epoch: 0011/15, cost =  0.281816214
Epoch: 0012/15, cost =  0.279919684
Epoch: 0013/15, cost =  0.277836859
Epoch: 0014/15, cost =  0.276022315
Epoch: 0015/15, cost =  0.274443209

Learning finished, Elapse test time :    69.0733seconds

• 모델 테스트

# 테스트 데이터를 사용하여 모델을 테스트한다.
with torch.no_grad(): # torch.no_grad()를 하면 gradient 계산을 수행하지 않는다.
    start = time()
    X_test = mnist_test.test_data.view(-1, 28 * 28).float().to(device)
    Y_test = mnist_test.test_labels.to(device)

    prediction = linear(X_test)
    correct_prediction = torch.argmax(prediction, 1) == Y_test
    accuracy = correct_prediction.float().mean()
    print(f'Evaluating finished, Elapse test time : {time() - start:10.4f}seconds')
    print(f'Accuracy: {accuracy.item()*100:.4}%' )

    # MNIST 테스트 데이터에서 무작위로 하나를 뽑아서 예측을 해본다
    r = random.randint(0, len(mnist_test) - 1)
    X_single_data = mnist_test.test_data[r:r + 1].view(-1, 28 * 28).float().to(device)
    Y_single_data = mnist_test.test_labels[r:r + 1].to(device)

    print('Label: ', Y_single_data.item())
    single_prediction = linear(X_single_data)
    print('Prediction: ', torch.argmax(single_prediction, 1).item())

    plt.imshow(mnist_test.test_data[r:r + 1].view(28, 28), cmap='Greys', interpolation='nearest')
    plt.show()

Evaluating finished, Elapse test time :     0.0279seconds
Accuracy: 88.68%
Label:  5
Prediction:  3

학습시킬 때 발생하는 문제점

• 신경망 모델에서 뉴런의 개수나 은닉층의 개수를 늘리기만 한다고 좋은 결과가 나오지 않은 이유는 크게 2가지로 볼 수 있음

• 경사 소실 문제(vanishing gradient problem)
• 오버피팅 문제(overfitting problem)

경사 소실 문제

• 신경망 모델을 학습시킬 때, 우리는 오차함수에 대한 최적해를 구하기 위해 매개변수의 경사를 구해야하는데 이 과정에서 경사가 없어져버리는($0$이 돼 버리는) 문제를 경사 소실 문제(vanishing gradient problem)라고 한다.

• 경사가 소실되면 오차 역전파법을 제대로 실행할 수가 없는데, 표 7.2와 같이 은닉층의 개수가 늘어날수록 경사 소실 문제가 현저하게 나타난다.

• 그림 7.3과 같이 은닉층이 2개인 신경망 모델을 생각해보면 각 층에서 나오는 뉴런의 출력은 각각 식 $(7.1)$, 식 $(7.2)$, 식 $(7.3)$과 같이 쓸 수 있다.
• $\mathbb{x}$ : 입력층의 값
• $\mathbb{h}_{(1)}, \mathbb{h}_{(2)}$ : 은닉층 2개
• $\mathbb{y}$ : 출력층의 값
• $\mathbf{W}, \mathbf{V}, \mathbf{U}$ : 각 층간의 웨이트 행렬
• $\mathbb{b}, \mathbb{c}, \mathbb{d}$ : 각 층의 바이어스 벡터
• $\sigma(\cdot)$ : 활성화를 시그모이드 함수

그림 7.2 은닉층이 2개인 4층 신경망 모델

$$\begin{align} \mathbb{h}_{(1)} &= \sigma(\mathbf{W}\mathbb{x} + \mathbb{b}) \tag{7.1}\\ \mathbb{h}_{(2)} &= \sigma(\mathbf{V}\mathbb{h}_{(1)} + \mathbb{c}) \tag{7.2}\\ \mathbb{y} &= \textrm{softmax}(\mathbf{U}\mathbb{h}_{(2)} + \mathbb{d}) \tag{7.3} \end{align}$$

• 다층 퍼셉트론을 모델화했을 때처럼 식 $(7.1)$과 식 $(7.2)$, 식 $(7.3)$을 다음과 같이 놓으면 웨이트 행렬 $\mathbf{W}=(\mathbb{w}_1, \mathbb{w}_2,\ldots, \mathbb{w}_J)$에 대한 경사는 식 $(7.7)$과 같이 나타낼 수 있다.

$$\begin{align} \mathbb{p} &= \mathbf{W}\mathbb{x} + \mathbb{b} \tag{7.4}\\ \mathbb{q} &= \mathbf{V}\mathbb{h}_{(1)} + \mathbb{c} = \mathbf{V}\big(\sigma(\mathbf{W}\mathbb{x} + \mathbb{c})\big) +\mathbb{c} = \mathbf{V}\cdot\sigma(\mathbb{p})+\mathbb{c}\tag{7.5}\\ \mathbb{r} &= \mathbf{U}\mathbb{h}_{(2)} + \mathbb{d} = \mathbf{U}\big(\sigma(\mathbf{V}\mathbb{h}_{(1)} + \mathbb{c})\big) +\mathbb{d} = \mathbf{U}\cdot\sigma(\mathbb{q}) +\mathbb{d}\tag{7.6} \end{align}$$

$$\begin{align} \frac{\partial E_n}{\partial \mathbb{w}_j} &= \frac{\partial E_n}{\partial \mathbb{p}_j} \frac{\partial \mathbb{p}_j}{\partial \mathbb{w}_j} \\&=\frac{\partial E_n}{\partial \mathbb{p}_j}\frac{\partial}{\partial \mathbb{w}_j}\Big(\not{\mathbf{W}}\mathbb{x}+\not{\mathbb{b}}\Big) \\ &=\frac{\partial E_n}{\partial \mathbb{p}_j}\mathbb{x} \tag{7.7}\end{align}$$

• 식 $(7.7)$에서 우리는 $\frac{\partial E_n}{\partial \mathbb{p}_j}$만 계산하면 되는데, 신경망 모델이 $3$층인 경우 편미분의 연쇄법칙(chain rule)을 적용하면 식 $(7.8)$과 식 $(7.9)$, 식 $(7.10)$과 같이 계산할 수 있다.

$$\begin{align} \frac{\partial E_n}{\partial \mathbb{p}_j} &= \sum_{k=1}^K \frac{\partial E_n}{\partial \mathbb{q}_k}\frac{\partial \mathbb{q}_k}{\partial \mathbb{p}_j}\tag{7.8}\\&= \sum_{k = 1}^K \frac{\partial E_n}{\partial \mathbb{q}_k}\frac{\partial}{\partial \mathbb{p}_j} \Big(\mathbf{V}\sigma(\mathbb{p})+\not{\mathbb{c}}\Big)\tag{7.9}\\&= \sum_{k=1}^K\frac{\partial E_n}{\partial \mathbb{q}_k}\Big(\mathbb{v}_{k_j}\sigma'(\mathbb{p}_j)\Big)\tag{7.10}\end{align}$$

• 신경망 모델이 $4$층인 경우에는 추가로 $\frac{\partial E_n}{\partial \mathbb{q}_k}$도 구해야 하기 때문에 편미분의 연쇄법칙을 한번 더 사용해서 식 $(7.11)$과 식 $(7.12)$, 식 $(7.13)$을 만들 수 있다.

$$\begin{align} \frac{\partial E_n}{\partial \mathbb{q}_k} &= \sum_{\ell=1}^L \frac{\partial E_n}{\partial \mathbb{r}_\ell}\frac{\partial \mathbb{r}_\ell}{\partial \mathbb{q}_k}\tag{7.11}\\&= \sum_{\ell = 1}^L \frac{\partial E_n}{\partial \mathbb{r}_\ell}\frac{\partial}{\partial \mathbb{q}_k} \Big(\mathbf{U}\sigma(\mathbb{q})+\not{\mathbb{d}}\Big)\tag{7.12}\\&= \sum_{\ell=1}^L\frac{\partial E_n}{\partial \mathbb{r}_\ell}\Big(\mathbb{u}_{\ell_k}\sigma'(\mathbb{q}_k)\Big)\tag{7.13}\end{align}$$

• $\frac{\partial E_n}{\partial \mathbb{r}_\ell}$은 출력층 부분이기 때문에 식 $(7.14)$와 같이 나타낼 수 있다.

$$ \frac{\partial E_n}{\partial \mathbb{r}_\ell} = -\Big(\mathbb{y}_\ell - H_\ell(\mathbb{x}_\ell)\Big)\tag{7.14}$$

• 식 $(7.14)$는 신경망 네트워크의 오차에 해당하기 때문에 오차를 다음과 같이 정의하면

$$\begin{align} \delta_j &= \frac{\partial E_n}{\partial \mathbb{p}_j}\tag{7.15} \\  \delta_k &= \frac{\partial E_n}{\partial \mathbb{q}_k}\tag{7.16}\\\delta_\ell &= \frac{\partial E_n}{\partial \mathbb{r}_\ell}\tag{7.17}\end{align}$$

• 식 $(7.15)$는 식 $(7.10)$과 식 $(7.13)$에 의해 다음과 같이 정리하면 4층 신경망 네트워크에서 사용할 수 있는 오차역전파법의 식 $(7.22)$얻을 수 있다.

$$\begin{align}\delta_j &= \frac{\partial E_n}{\partial \mathbb{p}_j} \tag{7.18}\\&= \sum_{k=1}^K \frac{\partial E_n}{\partial \mathbb{q}_k}\Big(\mathbb{v}_{k_j}\sigma'(\mathbb{p}_j)\Big)\quad\big(\because\,\, (7.10)\big)\tag{7.19}\\&= \sum_{k=1}^K\Bigg(\sum_{\ell=1}^L\frac{\partial E_n}{\partial \mathbb{r}_\ell} \Big(\mathbb{u}_{\ell_k} \sigma'(\mathbb{q}_k)\Big)\Bigg)\Big(\mathbb{v}_{k_j}\sigma'(\mathbb{p}_j)\Big)\quad\big(\because\,\, (7.13)\big)\tag{7.20}\\&= \sum_{k=1}^K\sum_{\ell=1}^L\delta_\ell \Big(\mathbb{u}_{\ell_k}\sigma'(\mathbb{q}_k)\Big)\Big(\mathbb{v}_{k_j}\sigma'(\mathbb{p}_{j})\Big)\quad\big(\because\,\, (7.17)\big)\tag{7.21}\\&= \sum_{k=1}^K\sum_{\ell=1}^L\Big(\mathbb{u}_{\ell_k}\mathbb{v}_{k_j}\Big)\Big(\sigma'(\mathbb{q}_k)\sigma'(\mathbb{p}_j)\Big)\delta_\ell \tag{7.22}\end{align}$$

• 이론적으로는 은닉층의 개수가 늘어도 편미분의 연쇄법칙을 반복해서 적용하면 정형화된 식을 통해 각 매개변수의 경사를 구할 수 있다.

• 그러나 식 $(7.22)$를 코드로 구현할 때에는 문제가 발생할 수 있는 부분이 있는데, 바로 뉴런의 활성화를 위한 시그모이드 함수가 사용되는 부분이다. 식 $(7.22)$ 오차역전파식에는 '시그모이드 함수를 미분한 것들의 곱' 부분이 있는데 우리는 시그모이드 함수를 미분하면 식 $(7.23)$이 되는 것을 알고 있으며, 이를 그래프로 나타내면 그림 $(7.3)$과 같다.

$$\sigma'(x) = \sigma(x)\big(1-\sigma(x)\big) \tag{7.23}$$

그림 7.3 시그모이드 함수 $\sigma(x)$와 시그모이드를 미분한 도함수 $\sigma'(x)$의 그래프

import numpy as np 
import matplotlib.pyplot as plt 

def sigmoid(x): 
    return 1 / (1 + np.exp(-x)) 
    
x = np.linspace(-10, 10, 1000) 
y = np.array([sigmoid(x) for x in x]) 
z = np.array([sigmoid(x)*(1-sigmoid(x)) for x in x]) 

plt.plot(x, y, label='$\sigma(x)$') 
plt.plot(x, z, label='$\sigma\'(x)$') 
plt.grid(linestyle='--', color='lavender') 
plt.legend() 
plt.show()

• 그림 $(7.3)$에서 알 수 있듯이 시그모이드 함수의 도함수 $\sigma'(x)$는 $x=0$일 때 최댓값 $\sigma'(x)=0.25$가 된다. 은닉층이 2개 있는 4층 신경망 모델에서 오류역전파 식 (7.22)의 값을 계산할 때에는 $0.25^2$이 곱해지는 것을 알 수 있으며, 은닉층이 $N$개인 경우에 오차를 계산할 때 $\alpha_N\leqq 0.25^N < 1$ 범위에 있는 $\alpha_N$이 곱해진다는 것을 알 수 있으며 $N$이 커지면 $\alpha_N$ 또한 $0$에 수렴하는 것을 알 수 있다.

$$\lim_{N\rightarrow\infty}{\alpha_N} = \lim_{N\rightarrow\infty} \Bigg(\frac{1}{4}\Bigg)^N=0 \tag{7.24}$$

• 은닉층이 많아지면 오류역전파식을 통해 오차를 계산할 때 식 $(7.24)$로 인하여 오차항의 값이 $0$에 가까워지는 현상을 경사 소실 문제(vanishing gradient problem)이라고 하며, 이를 해결하기 위해서는 미분을 하더라도 값이 작아지지 않는 활성 함수를 사용해야만 한다.

• 또한 경사 소실 문제는 은닉층이 많지 않더라도 발생할 수 있는데, 각 층의 차원(뉴런의 수)이 높아지는 경우에 시그모이드 함수를 통해 활성화되는 $\mathbf{W}\mathbb{x}+\mathbb{b}$의 값이 커질 수 있어 경사가 소실될 수 있다.
• $\mathbf{W}=(\mathbb{w}_1, \mathbb{w}_2, \ldots, \mathbb{w}_n)$이라고 하면 그림 $(7.3)$에서 알 수 있듯이 시그모이드 함수의 입력값이 커지기 때문에 식 $(7.25)$가 성립한다. 따라서 식 $(7.26)$으로 인해 경사가 소실될 수 있다.

$$\lim_{n\rightarrow\infty} \sigma\big(\mathbf{W}\mathbb{x}+\mathbb{b}\big) = 1 \tag{7.25}$$

$$\begin{align}\lim_{n\rightarrow\infty} \sigma'\big(\mathbf{W}\mathbb{x}+\mathbb{b}\big) &= \lim_{n\rightarrow\infty}\sigma\big(\mathbf{W}\mathbb{x}+\mathbb{b}\big)(1-\sigma(\mathbf{W}\mathbb{x}+\mathbb{b})) \\&= 1\cdot(1-1)\\&=0 \tag{7.26}\end{align}$$

오버피팅 문제

• 오버피팅(overfitting)은 예측 모델이 학습 데이터에만 최적화되어 테스트 데이터를 제대로 예측하지 못하는 상태를 말하며 과학습 또는 과잉적합이라고도 한다.

• 오버피팅의 예를 설명하기 위해 그림 $7.4$와 같이 실제 분포는 $f(x)=\cos(\fracx)$일 때, 이 분포를 따르는 30개의 데이터가 있다고 해보자.

그림 7.4 $f(x)=\cos(\frac{3\pi}{2}x)$ 분포를 따르는 30개의 샘플 데이터

import numpy as np 
import matplotlib.pyplot as plt 

M = 2 
e = np.random.randn(30) * 0.1 

x = np.linspace(0, 1, 100) 
y = np.cos(3*np.pi / 2 * x) 

x1 = np.sort(np.random.choice(x, 30, replace=False)) 
y1 = np.cos(3*np.pi / 2 * x1) + e 

plt.scatter(x1, y1, facecolor='red', label='sample data') 
plt.plot(x, y, color='lightgrey', label='$\cos(/x)$') 
plt.grid(linestyle='--', color='lavender') 
plt.legend()
plt.show()

• 30개의 샘플 데이터를 보고 분포 $\cos(\frac{3\pi}{2}x)$ 모델을 찾을 수 있으면 좋겠지만 실제로는 학습 데이터만 보고 모델을 찾는 것이 쉽지 않다.
• 데이터 분류 및 예측을 위한 신경망 모델은 학습 데이터를 통해 가능한 한 실제 분포 함수와 가까운 함수로 근사해서 예측 정확도를 높여야 하기 때문에 근사치를 구하기 위해 사용되는 함수를 어떻게 설정하는지가 중요하다.
• 식 $(7.27)$과 같은 다항식 함수로 회귀분석 하는 방법을 생각해보자.

$$\begin{align} \hat{f}(x) &=a_0+a_1x + a_2x^2+ \cdots + a_nx^n\\&= \sum_{i=0}^na_ix^i\tag{7.29}\end{align}$$

• $n=1$일 경우에 $\hat(x)=a_0+a_1x$이기 때문에 직선으로 표현되며, $n=2$인 경우에는 2차 함수 곡선으로 표현할 수 있다. 따라서 $n$을 크게하면 더 복잡한 곡선을 표현할 수 있는데, 실제로는 $n$을 크게 하더라도 정확하게 표현하는 것이 쉽지 않다.

• 그림 $7.5$는 $n=1, 4, 33$일 때 30개의 샘플 데이터를 사용해 회귀 분석한 것으로 $n=1$일 때에는 직선으로 표현할 수 밖에 없어 샘플 데이터를 제대로 표현할 수가 없으며, $n=33$일 때에는 더욱 복잡한 함수를 표현할 수 있지만 샘플 데이터만 표현하는 것에 맞춰 회귀되었기 때문에 결과적으로는 실제 분포인 $\cos(\frac{3\pi}{2}x)$와는 다소 거리가 있다.
  

그림 7.5 1차 함수 회귀(왼쪽), 4차 함수 회귀(중간), 33차 함수로 회귀(오른쪽)

• 이는 샘플 데이터의 개수가 한정돼 있기 때문에 주어진 데이터만 잘 표현할 수 있는 분포 함수를 찾았다고 하더라도 이 분포 함수가 새롭게 발생되는 미지의 데이터도 잘 표현할 수 있도는 장담을 할 수가 없다. $n=33$일 때처럼 샘플 데이터만을 과잉으로 회귀하는 상태를 오버피팅이라고 한다.

• 은닉층이나 은닉층의 뉴런 개수를 늘려도 신경망 모델을 구성하는 전체 뉴런의 개수가 늘어나기 때문에 더욱 복잡한 패턴을 표현할 수 있지만 학습 데이터만을 복잡한 방법으로 표현한다면 데이터의 실제 분포와는 다른 패턴 분류의 형태가 될 가능성이 높아진다.

• 신경망 모델을 학습시킬 때는 오차 함수 $E$값이 최소가 되도록 매개변수 값을 변경했지만 단순히 $E$를 최소화하면 오버피팅될 가능성이 있기 때문에 무조건 최소화시키기만 하면 좋은 것은 아니다.

• 학습 데이터는 예측이 잘 되지만 테스트 데이터는 예측이 잘 안된다면 오버피팅을 의심해봐야만 한다.

출처 : 정석으로 배우는 딥러닝

비선형 분류(Non-Linear Classification)

• XOR(배타논리) 게이트는 아래 그림과 같으며 입출력은 아래 표와 같다
  

• XOR 게이트를 좌표평면 상에 그래프로 나타내면 아래 그림처럼 AND 게이트나 OR 게이트와는 달리 직선 하나로 데이터를 분류할 수 없다

출처 : http://solarisailab.com/wp-content/uploads/2017/05/xor_limitation.gif

• XOR 게이트의 데이터를 분류하기 위해서는 적어도 2개의 데이터가 필요

출처 : http://needjarvis.tistory.com/181

• AND 게이트나 OR 게이트처럼 직선 하나($K$ 클래스인 경우에는 $K-1$개의 직선)으로 데이터를 분류하는 것을 '선형 분리 가능(linearly seperable)하다'고 하며 XOR 게이트처럼 직선 하나로 분류할 수 없는 경우를 '선형 분리 불가능(linearly non-seperable)하다'고 한다

• 단순 퍼셉트론이나 로지스틱 회귀처럼 선형 분리 가능한 문제에만 적용할 수 있는 모델을 선형 분류기(linear classifier)라고 한다
• 데이터가 $n$차원인 경우에는 $n-1$차원의 초평면으로 분리가 가능한지 알아봐야 하며, 분리가 안되는 경우에는 데이터의 차원을 강제로 높여서 더 높은 차원의 초평면으로 분리하는 방법 중의 하나가 SVM(Support Vector Machine) 알고리즘

XOR 게이트 구현을 위하여 게이트 조합하기

• AND, OR, NOT의 기본 게이트들은 선형 분리 가능하기 때문에 이들을 아래 그림과 같이 조합하여 구현하면 선형 분리 불가능한 XOR 게이트를 선형으로 분리할 수 있다

• XOR 게이트를 기본 게이트들의 조합으로 구성할 수 있다는 것은 신경망 모델에서 있어서 매우 중요
• 뉴런을 기본 게이트로 구성할 수 있기 때문에 비선형 분류를 할 수 있는 뉴런 모델을 기본 게이트의 조합으로 구현 가능
• 비선형 분류를 위해서는 여태까지 구현했던 것처럼 입력과 출력만 생각해서는 안된다
• 기존 신경 모델에 아래 그림 6.1처럼 점선 내부에 기본 게이트들을 추가한다

그림 6.1  기본 게이트를 조합해서 만든 XOR 게이트 모델

• 위 그림 6.1에서 점선 부분만 따로 뗴어내면 입력이 2개, 출력이 2개이 때문에 신경망 모델에서는 아래 그림 6.2처럼 2개의 뉴런을 추가하여 위 그림 6.1의 점선 부분처럼 입력이 2개, 출력도 2개로 나타낼 수 있다

그림 6.2  XOR 게이트를 신경망으로 구현한 모델

신경망 모델이 XOR 게이트를 제대로 구현한 것인가?

• 위에서 구현한 신경망 모델 그림 6.2가 XOR 게이트를 제대로 재현한 것인지 검증해보자

• 위 그림 6.2의 신경망 모델에서 뉴런의 구조는 우리가 앞에서 해왔던 것에서 변한 것이 없기 때문에 식 (6.1)과 식 (6.2), 식 (6.3)으로 나타낼 수 있다

\begin{align}h_1 &= f(w_{11}x_1+w_{12}x_2+b_1) \tag{6.1}\end{align}

\begin{align}h_2 &= f(w_{21}x_1+w_{22}x_2+b_2) \tag{6.2}\end{align}

\begin{align}y &=f(v_1h_1 + v_2h_2+c) \tag{6.3}\end{align}

• 그림 6.1에 맞추기 위해 우리는 활성화 함수 $f(\cdot)$로 계단 함수를 사용하겠지만 지금까지 살펴본 것처럼 함수의 내용이 양이냐 음이냐에 따라 출력값이 정해진다는 점에서 시그모이드 함수를 사용해도 문제되지 않는다

• 식 (6.1)과 식 (6.2), 식 (6.3)에 다음의 값을 대입하면 식 (6.4)와 식 (6.5), 그리고 신경망 모델의 가설식 (6.6)을 얻을 수 있다
  

\begin{eqnarray} W=\left( \begin{array}{cc} w_{11} & w_{12} \\ w_{21} & w_{22} \end{array}\right) = \left( \begin{array}{rr} 2 & 2 \\ -2 & -2 \end{array}\right)\end{eqnarray}

\begin{align} b= \left(\begin{array}{c}b_1 \\ b_2 \end{array}\right) = \left(\begin{array}{c} 2 \\ 2 \end{array}\right)\end{align}

\begin{align} v= \left(\begin{array}{c}v_1 \\ v_2 \end{array}\right) = \left(\begin{array}{c} 2 \\ 2 \end{array}\right)\end{align}

\begin{align} c = -3 \end{align}

\begin{align}h_1 &= f(2x_1+2x_2-1) \tag{6.1}\end{align}

\begin{align}h_2 &= f(-2x_1-2x_2+3) \tag{6.2}\end{align}

\begin{align}H(x) &=f(2h_1 +2h_2-3) \tag{6.3}\end{align}

• 식 (6.4)와 식 (6.5), 식 (6.6)을 토대로 XOR 게이트의 입력값을 계산해보면 가설식의 출력이 XOR 게이트의 출력과 같기때문에 신경망으로 XOR 게이트를 재현할 수 있다는 것을 알 수 있다
  

• 다층 퍼셉트론(MLP; Multi-Layer Perceptron) : 입력과 출력 이외의 뉴런이 연결된 모델
  

• 다층 퍼셉트론이라는 이름에서 알 수 있듯이 신겸앙 모델은 인간의 뇌와 마찬가지로 뉴런이 층을 이루어 연결되어 있다고 생각할 수 있다
• 입력층(Input Layer) : 입력을 받는 층
• 출력층(Output Layer) : 출력하는 층
• 은닉층(Hidden Layer) : 입력층과 출력층 사이에 추가된 층

다층 퍼셉트론의 모델링

• '입력층 - 은닉층 - 출력층'이라는 3층 네트워크 구조로 만들면 XOR 게이트처럼 선형 분리 불가능한 데이터도 분리 가능하기 때문에 MLP 모델을 일반화하면 더욱 복잡한 데이터도 분류 가능
  

• MLP 모델의 일반화를 위해 3층 신경망을 일반화했을 때의 모델은 그림 6.3과 같이 나타낼 수 있다
  

그림 6.3  3층 신경망 구조

• '입력층 - 은닉층' 부분만 따로 살펴보면 지금까지 봐왔던 신경망 모델과 같은 모양이기 때문에 은닉층의 출력을 나타나는 식은 가중치 $\boldsymbol{W}$, 바이어스 $\mathbb{b}$, 활성화 함수 $f(\cdot)$일 때, 식 (6.7)과 같다

\begin{eqnarray} \mathbb{h} = f(\boldsymbol{W}\mathbb{x} + \mathbb{b})\tag{6.7}\end{eqnarray}

• 식 (6.7)로 구한 $\mathbb{h}$는 출력층에 대하여 입력층으로 전기신호를 전달하기 때문에 '은닉층 - 출력층' 부분은 가중치 $\boldsymbol{V}$, 바이어스 $\mathbb{c}$, 활성화 함수 $g(\cdot)$일 때, 식 (6.8)과 같으며, 이를 가설식으로 만들면 식 (6.9)로 표기할 수 있다

\begin{eqnarray} y = g(\boldsymbol{V}\mathbb{h} + \mathbb{c})\tag{6.8}\end{eqnarray}

\begin{eqnarray} H(\mathbb{x}) = g(\boldsymbol{V}\mathbb{h} + \mathbb{c})=g\big(\boldsymbol{V}\cdot f(\boldsymbol{W}\mathbb{x} + \mathbb{b}) +\mathbb{c}\big)\tag{6.9}\end{eqnarray}

• 활성화 함수 $g$는 신경망 모델의 전체 출력이기 때문에 다중 클래스 분류를 할 때에는 소프트맥스 함수를 사용하면 되고, 이진 분류를 하는 경우에는 시그모이드 함수를 사용하면 된다

• 활성화 함수 $f$는 출력층에 신호를 전달하는 역할을 하며, $g(\cdot)$ 안에 있는 $\boldsymbol{V}\mathbb{h}+\mathbb{c}$는 임의의 실수이기만 하면 되기 때문에 $\mathbb{h}$를 출력하는 활성화 함수 $f$는 입력값이 작으면 출력도 작은 값을 출력하고, 입력값이 크면 출력도 큰 값을 출력하는 함수이면 충분하지만 계산의 편의성을 위해 시그모이드 함수를 사용한다

다층 신경망 모델식 최적화 문제와 역전파 모델

• 다층 신경망 모델에서 학습을 시킨다하는 것은 식 (6.9) 가설식과 실제의 값 $\mathbb{y}$의 차를 최소로 만드는 매개변수 $\boldsymbol{W}$와 $\boldsymbol{V}$, $\mathbb{b}$, $\mathbb{c}$를 찾는 최적화 문제가 되는데, 신경망 모델의 핵심이 되는 오차 역전파 모델에 대해 자세히 알아보기 위해 각 층에 있는 웨이트 행력을 벡터로 분해해서 경사하강법 모델을 해석해보자
  

• 오차함수를 $E$라고 하면 $E=E(\boldsymbol{W}, \boldsymbol{V}, \mathbb{b}, \mathbb{c})$가 되며, 이 때 경사하강법을 통해 가장 적합한 매개변수를 찾으면 된다

• 각 매개변수에 관한 경사를 구하기 위해여, 각각의 매개변수로 편미분을 구해야하기 때문에 지금까지 한 것처럼 $N$개의 입력 데이터가 있다고 가정하고 그 중에서 $n$번째에 해당하는 데이터 벡터를 $x_n$과 $y_n$이라고 하자

• $N$개의 데이터 각각에서 발생하는 오차 $E_n$ $(n=1,2,\ldots,N)$은 서로 독립적으므로 식 (6.10)과 같이 나타낼 수 있다

\begin{eqnarray} E = \sum_{n=1}^N E_n \tag{6.10}\end{eqnarray}

• 은닉층과 출력층에서 활성화되기 이전의 값을 각각 식 (6.11)과 식 (6.12)로 표현할 수 있다

\begin{align} \mathbb{p} = \boldsymbol{W}\mathbb{x} + \mathbb{b}\tag{6.11}\end{align}

\begin{align} \mathbb{q} = \boldsymbol{V}\mathbb{h} + \mathbb{c}\tag{6.12}\end{align}

• $\boldsymbol{W}=(\mathbb{w}_1,\mathbb{w}_2,\ldots,\mathbb{w}_J)$와 $\boldsymbol{V}=(\mathbb{v}_1,\mathbb{v}_2,\ldots,\mathbb{v}_K)$에 대해 각각 식 (6.11)과 식 (6.12)에 의해서 식 (6.13)과 식 (6.14)가 성립한다

\begin{eqnarray} \left\{\begin{array}{l}\frac{\partial E_n}{\partial \mathbb{w}_j} = \frac{\partial E_n}{\partial \mathbb{p}_j} \frac{\partial \mathbb{p}_j}{\partial \mathbb{w}_j} = \frac{\partial E_n}{\partial \mathbb{p}_j}\mathbb{x}\\\frac{\partial E_n}{\partial \mathbb{b}_j} = \frac{\partial E_n}{\partial \mathbb{p}_j} \frac{\partial \mathbb{p}_j}{\partial \mathbb{b}_j} = \frac{\partial E_n}{\partial \mathbb{p}_j}\end{array}\right.\tag{6.13}\end{eqnarray}

\begin{eqnarray} \left\{\begin{array}{l}\frac{\partial E_n}{\partial \mathbb{v}_k} = \frac{\partial E_n}{\partial \mathbb{q}_k} \frac{\partial \mathbb{q}_k}{\partial \mathbb{v}_k} = \frac{\partial E_n}{\partial \mathbb{q}_k}\mathbb{h}\\\frac{\partial E_n}{\partial \mathbb{c}_k} = \frac{\partial E_n}{\partial \mathbb{q}_k} \frac{\partial \mathbb{q}_k}{\partial \mathbb{c}_k} = \frac{\partial E_n}{\partial \mathbb{q}_k}\end{array}\right.\tag{6.14}\end{eqnarray}

• 식 (6.13)과 식 (6.14)에서 $\frac{\partial E_n}{\partial \mathbb{p}_j}$와 $\frac{\partial E_n}{\partial \mathbb{q}_k}$를 구하면 매개변수 $\boldsymbol{W}$와 $\boldsymbol{V}$에 대한 경사, 즉 편미분을 구할 수 있다

• 식 (6.14)에서 $\frac{\partial E_n}{\partial \mathbb{q}_k}$를 계산해보자

• '은닉층 - 출력층' 부분에서 활성화 함수로 소프트맥스 함수를 사용하기 때문에 다중 클래스 로지스틱 회귀 모델링에서 계산했던 방법(식 (6.16)~식 (6.23))을 사용하면 식 (6.15)를 얻을 수 있다

\begin{align} \frac{\partial E_n}{\partial \mathbb{q}_k} = - (\mathbb{y}_{n_k} - H_{n_k}(\mathbb{x}_n))\quad(\because\,\, H_{n_k}(\mathbb{x}_n)=g(\mathbb{q}_k)\,\,(6.12)) \tag{6.15}\end{align}

복습 : 다중 클래스 분류 모델의 편미분 계산

• 입력 데이터 $\mathbb{x}$가 어떤 클래스$(k)$로 분류될 확률 변수를 $C$라고 하면

• 이진 분류의 경우 : $C\in \{0,1\}$
• 다중 클래스 분류의 경우 : $C = k$ $(k=1, 2, \ldots, K)$
• 다중 클래스 분류를 위해 소프트맥스 함수를 사용하기 때문에 $\mathbb{y}_k$는 식 (6.16)과 같다

\begin{align} \mathbb{y}_k &= \textrm{softmax}(\mathbb{x})_n\,\,(n=1, 2, \ldots, N)\\&=\frac{e^{\mathbb{x}_i}}{\sum_{j=1}^ne^{\mathbb{x}_j}}\tag{6.16}\end{align}

• 이제 '은닉층 - 출력층' 부분에서 입력 데이터 $\mathbb{h}_j=f(\boldsymbol{W}\mathbb{x}_n+\mathbb{b})$가 어떤 클래스($\mathbb{y}_k)$로 분류될 확률은 $g(\cdot)$이 소프트맥스 함수이기 때문에 식 (6.17)로 표현할 수 있다

\begin{align} \textrm{Pr} (C=k|\mathbb{h}_j) &= \frac{e^{\mathbb{h}_j}}{\sum_{i=1}^Je^{\mathbb{h}_j}} \tag{6.17}\end{align}

• $\mathbb{h}_j$ $(j=1, 2, \ldots, J)$가 $k$ 클래스에 속한다면 $\mathbb{y}_j$의 $k$번째 성분인 $\mathbb{y}_{j_k}$는 $1$이지만 그 외의 $\ell\neq k$번째 성분인 $\mathbb{y}_{j_\ell}$은 $0$이기 때문에 식 (6.18)과 같이 1-of-$K$ 표현으로 나타낼 수 있다
  

\begin{eqnarray} \mathbb{y}_{j_{\ell}} = \left\{\begin{array}{lc} 1 & (\ell = k) \\ 0 & (\ell\neq k)\end{array}\right.\tag{6.18}\end{eqnarray}

• '은닉층 - 출력층' 부분에서 다중 클래스 분류 모델의 가설식이 식 (6.9)이고, 이 때 다중 클래스 분류 문제이기 때문에 $g(\cdot)$이 소프트맥스 함수이기 때문에 $\boldsymbol{V}$와 $\mathbb{c}$의 가장 좋은 값을 찾기 위한 가능도 함수는 식 (6.19)로 표현할 수 있다
• 각각의 $\mathbb{h}_j=f(\boldsymbol{W}\mathbb{x}_n+\mathbb{b})$에 대하여 신경망 모델의 출력값이 $\mathbb{y}_{j_k}$이 될 확률 $\textrm{Pr}(C=k|\mathbb{h}_j)$이 높아야 좋은 모델이다
  

\begin{align} L(\boldsymbol{V}, \mathbb{c}) &= \prod_{j=1}^J\prod_{k=1}^K\textrm{Pr}(C=k|\mathbb{h}_j)^{\mathbb{y}_{j_k}}\\ &= \prod_{j=1}^J\prod_{k=1}^K\big(g_{j_k}(\mathbb{h}_j)\big)^{\mathbb{y}_{j_k}}\tag{6.19}\end{align}

• 식 (6.19)을 최대로 만드는 매개변수 $\boldsymbol{V}$와 $\mathbb{c}$를 구하기 위해 식 (6.19)에 $\log$를 취하는 변형을 하면 식 (6.20)을 얻을 수 있다

\begin{align} E(\boldsymbol{V}, \mathbb{c}) &= -\log L(\boldsymbol{V}, \mathbb{c})\\ &= -\sum_{j=1}^J \sum_{k=1}^{K}\mathbb{y}_{j_k}\log g_{j_k}(\mathbb{h}_j)\tag{6.20}\end{align}

• 우리는 식 (6.20)이 교차 엔트로피 오차 함수로 이 식의 최적화 문제를 풀어야 가설식이 맞는 매개변수를 찾을 수 있다는 것을 알고 있다. 그리고 가장 널리 알려진 경사하강법을 통해 최적화된 매개변수를 찾을 수 있다는 것도 알고 있다

복습 : 다중 클래스 회귀 모델의 경사하강법

• '은닉층 - 출력층' 부분에서 $\mathbb{q}$의 $\ell$번째 성분인 $\mathbb{q}_\ell$의 편미분을 구해보자

• $I$를 $K$차 단위행렬이라고 하면 다음과 같이 식 (6.21)을 얻을 수 있다

\begin{align} \frac{\partial E_n}{\partial \mathbb{q}_\ell} &= -\sum_{j=1}^J\sum_{k=1}^K \frac{\partial E_n}{\partial g_{j_k}(\mathbb{q}_j)}\frac{\partial g_{j_k}(\mathbb{q}_j)}{\partial \mathbb{q}_\ell}\\  &= -\sum_{j=1}^J\sum_{k=1}^K \frac{\partial}{\partial g_{j_k}(\mathbb{q}_j)} \big(\mathbb{y}_{j_k}\log g_{j_k}(\mathbb{q}_j)\big)\frac{\partial g_{j_k}(\mathbb{h}_j)}{\partial \mathbb{q}_\ell}\quad(\because\,\, (6.20))\\ &= -\sum_{j=1}^J\sum_{k=1}^K \frac{\mathbb{y}_{j_k}}{\log g_{j_k}(\mathbb{h}_j)} \frac{\partial g_{j_k}(\mathbb{h}_j)}{\partial \mathbb{q}_\ell}\\ &= -\sum_{j=1}^J\sum_{k=1}^K \frac{\mathbb{y}_{j_k}}{\log g_{j_k}(\mathbb{x}_n)} g_{j_k}(\mathbb{h}_j)\big(I_{j_k} - g_{j_k}(\mathbb{h}_j)\big)\quad(\because\,\, g_{j_k}(\mathbb{h}_j)\textrm{ is softmax})\\ &= -\sum_{j=1}^J \Bigg(\sum_{k=1}^K \mathbb{y}_{j_k} I_{j_k} - \sum_{k=1}^K \mathbb{y}_{j_k}g_{j_k}(\mathbb{h}_j)\Bigg)\\ &= -\sum_{j=1}^J \big(\mathbb{y}_{j_\ell} - g_{j_\ell}(\mathbb{h}_j)\big)\quad(\because\,\,(6.18))\\ &= -\big(\mathbb{y}_\ell - g_\ell(\mathbb{h}_j)\big)\quad(\because\,\,(6.18))\tag{6.21}\end{align}

다층 신경망 모델식 최적화 문제와 역전파 모델(계속)

• '은닉층 - 출력층' 부분의 편미분 식 (6.14)는 식 (6.21)로부터 식 (6.22)로 다시 쓸 수 있는데, 이는 지금까지 우리가 봐왔던 식과 동일한 것을 알 수 있다

\begin{align} \frac{\partial E_n}{\partial \mathbb{v}_k} &= \frac{\partial E_n}{\partial \mathbb{q}_k}\mathbb{h}= -\big(\mathbb{y}_\ell - g_\ell(\mathbb{h}_j)\big)\mathbb{h}\tag{6.22} \end{align}

• 이제 우리는 식 (6.13)의 $\frac{\partial E}{\partial \mathbb{p}_j}$를 구하면 식 (6.23)가 되기 때문에 모든 경사를 구할 수가 있다
  

\begin{align} \frac{\partial E_n}{\partial \mathbb{p}_j} &= \sum_{k=1}^K \frac{\partial E_n}{\partial \mathbb{q}_k} \frac{\partial \mathbb{q}_k}{\partial \mathbb{p}_j} \\ &= \sum_{k=1}^K \frac{\partial E_n}{\partial \mathbb{q}_k} \frac{\partial}{\partial \mathbb{p}_j}\big(\mathbb{v}_{k_j}f(\mathbb{p}_j)+\mathbb{c}_k \big) \quad(\because\,\, \mathbb{q}=\boldsymbol{V}f(\mathbb{p})+\mathbb{c})\\ &= \sum_{k=1}^K \frac{\partial E_n}{\partial \mathbb{q}_k} \Big( f'(\mathbb{p}_j)\mathbb{v}_{kj}\Big)\tag{6.23}\end{align}

• 식 (6.13)과 식 (6.14)를 식 (6.24)와 식 (6.25)로 정의해보면 $\delta_k$는 식 (6.21)에 의해 정답과 모델 가설식 값과의 차이이기 때문에 $\delta_k$나 $\delta_j$를 오차라고도 할 수 있다

\begin{align} \delta_j &= \frac{\partial E_n}{\partial \mathbb{p}_j} \tag{6.24}\\ \delta_k &= \frac{\partial E_n}{\partial \mathbb{q}_k} \tag{6.25}\end{align}

• 식 (6.24)와 식 (6.25)는 다시 각각 식 (6.26)과 식 (6.27)로 다시 정리할 수 있다

\begin{align} \delta_j &= \frac{\partial E_n}{\partial \mathbb{p}_j}\\ &= \sum_{k=1}^K \frac{\partial E_n}{\partial \mathbb{q}_k} \Big( f'(\mathbb{p}_j)\mathbb{v}_{kj}\Big) \\ &= f'(\mathbb{p}_j) \sum_{k=1}^K \mathbb{v}_{k_j}\delta_k\tag{6.26}\\ \delta_k &= \frac{\partial E_n}{\partial \mathbb{q}_k} \\&= -\big(\mathbb{y}_\ell - g_\ell(\mathbb{h}_j)\big)\tag{6.26}\end{align}

• 식 (6.26)에서 $\sum_{k=1}^K \mathbb{v}_{k_j}\delta_k$ 부분만 따로 떼어내 살펴보면 지금까지 살펴봤던 뉴런의 출력을 나타내는 식과 모양이 같은 것을 알 수 있다. 이는 다시 말하면 신경망 모델에서 네트워크의 입력층에서 출력층으로 향하는 순방향전파(forward propagation) 출력 모델식을 고려해 해석학적으로 살펴봤지만 오차함수 최적화를 위해 매개변수를 업데이트하기 위한 경사하강법을 해석할 때에는 그림 6.4처럼 $\delta_k$가 네트워크 상에서 출력층에서 입력층으로 전파되는 모델(error backpropagation)로 생각할 수 있다

그림 6.4  오차가 출력층에서 은닉층을 통해 입력층으로 역전파되는 모델

웨이트 행렬을 벡터로 분해하지 않고 기울기 계산하기

• 교차 엔트로피 오차 함수를 웨이트로 직접 미분을 하면 다음과 같은 식을 얻을 수 있다

\begin{align} \frac{\partial E_n}{\partial \boldsymbol{W}} &= \frac{\partial E_n}{\partial \mathbb{p}}\Big(\frac{\partial \mathbb{p}}{\partial \boldsymbol{W}}\Big) \\ &= \frac{\partial E_n}{\partial \mathbb{p}}\mathbb{x}\tag{6.27}\end{align}

\begin{align} \frac{\partial E_n}{\partial \boldsymbol{V}} &= \frac{\partial E_n}{\partial \mathbb{q}}\Big(\frac{\partial \mathbb{q}}{\partial \boldsymbol{V}}\Big) \\ &= \frac{\partial E_n}{\partial \mathbb{q}}\mathbb{h}\tag{6.28}\end{align}

• 다음과 같이 정의되는 $\mathbb{e}_\mathbb{p}$와 $\mathbb{e}_\mathbb{q}$는 각각 $\delta_j$와 $\delta_k$를 성분으로 하는 벡터이다

\begin{align} \mathbb{e}_\mathbb{p} = \frac{\partial E_n}{\partial \mathbb{p}}\tag{6.29}\end{align}

\begin{align} \mathbb{e}_\mathbb{q} = \frac{\partial E_n}{\partial \mathbb{q}}\tag{6.30}\end{align}

• 따라서 다음과 같은 식을 얻을 수 있다

\begin{align} \mathbb{e}_\mathbb{p} = f'(\mathbb{p})\odot \boldsymbol{V}\mathbb{e}_\mathbb{q}\tag{6.30}\end{align}\begin{align} \mathbb{e}_\mathbb{q} = -(\mathbb{y} - g(\mathbb{h}))\tag{6.31}\end{align}

TensorFlow로 XOR 게이트 구현

import numpy as np
import tensorflow as tf

X = np.array([[0, 0],
              [0, 1],
              [1, 0],
              [1, 1]])
Y = np.array([[0],
              [1],
              [1],
              [0]])

x = tf.placeholder(tf.float32, shape=[None, 2])
y = tf.placeholder(tf.float32, shape=[None, 1])

• 입력층 - 은닉층 설계
• tf.trunated_normal()은 절단정규분포(truncated normal distribution)를 따르는 데이터를 생성
• tf.zeros()로 매개변수를 모두 0으로 초기화하고 오차역전파법을 적용하면 오차가 제대로 반영되지 않을 경우가 있어 절단정규분포를 사용한다는데 결과가 잘 안나온다. random_normal()로 바꿔도 잘 안된다. 뭐가 문제일까?
  

# 입력층 - 은닉층
W = tf.Variable(tf.truncated_normal([2, 2]))
b = tf.Variable(tf.zeros([2]))
h = tf.nn.softmax(tf.matmul(x, W) + b)

• 은닉층 - 출력층 설계

# 은닉층 - 출력층
V = tf.Variable(tf.truncated_normal([2, 1]))
c = tf.Variable(tf.zeros([1]))
hypothesis = tf.nn.sigmoid(tf.matmul(h, V) + c)

• 신경망 모델 구현

cost = -tf.reduce_sum(y * tf.log(hypothesis) + (1-y) * tf.log(1-hypothesis))
train = tf.train.GradientDescentOptimizer(learning_rate=0.1).minimize(cost)
accuracy = tf.equal(tf.to_float(tf.greater(hypothesis, 0.5)), y)

init = tf.global_variables_initializer()
sess = tf.Session()
sess.run(init)

for epoch in range(4000):
    sess.run(train, feed_dict={x: X, y: Y})

    if epoch % 1000 == 0:
        print(f'STEP = {epoch}')

classified = accuracy.eval(session=sess, feed_dict={x: X, y: Y})

prob = hypothesis.eval(session=sess, feed_dict={x: X})

print(f'classified:\n{classified}')
print()
print(f'output probability:\n{prob}')

STEP = 0
STEP = 1000
STEP = 2000
STEP = 3000
classified:
[[ True]
 [ True]
 [ True]
 [ True]]

output probability:
[[0.00680913]
 [0.99074006]
 [0.9909436 ]
 [0.00837671]]

Keras로 XOR 게이트 구현

import numpy as np
from keras.models import Sequential
from keras.layers import Dense, Activation
from keras.optimizers import SGD

X = np.array([[0, 0],
              [0, 1],
              [1, 0],
              [1, 1]])
Y = np.array([[0],
              [1],
              [1],
              [0]])

model = Sequential()

# 입력층 - 은닉층
model.add(Dense(input_dim=2, units=2))
model.add(Activation('sigmoid'))

# 은닉층 - 출력층
model.add(Dense(units=1))
model.add(Activation('sigmoid'))

model.compile(loss='binary_crossentropy', optimizer=SGD(lr=0.1))

model.fit(X, Y, epochs=4000, batch_size=4)

classes = model.predict_classes(X, batch_size=4)
prob = model.predict_proba(X, batch_size=4)

print(f'classified:\n{Y==classes}')
print()
print(f'output probability:\n{prob}')

4/4 [==============================] - 0s 0us/step - loss: 0.1658
Epoch 3993/4000

4/4 [==============================] - 0s 251us/step - loss: 0.1656
Epoch 3994/4000

4/4 [==============================] - 0s 251us/step - loss: 0.1654
Epoch 3995/4000

4/4 [==============================] - 0s 0us/step - loss: 0.1652
Epoch 3996/4000

4/4 [==============================] - 0s 0us/step - loss: 0.1650
Epoch 3997/4000

4/4 [==============================] - 0s 250us/step - loss: 0.1648
Epoch 3998/4000

4/4 [==============================] - 0s 250us/step - loss: 0.1647
Epoch 3999/4000

4/4 [==============================] - 0s 0us/step - loss: 0.1645
Epoch 4000/4000

4/4 [==============================] - 0s 250us/step - loss: 0.1643
classified:
[[ True]
 [ True]
 [ True]
 [ True]]

output probability:
[[0.17661843]
 [0.86831385]
 [0.85175645]
 [0.14821118]]

출처 : 정석으로 배우는 딥러닝

소프트맥스 함수를 이용하는 다중 클래스 로지스특 회귀

소프트맥스 함수(Softmax Function)

• 신경망에서 출력이 발화한다/안한다 2가지인 경우보다는 더욱 많은 경우를 분류하거나 예측해야하는 문제가 더 많음

• 데이터를 2가지 분류하는 문제를 이진 분류(binary classification)이라 하고 3개 이상으로 분류하는 문제를 다중클래스 분류(multiclass classification)라 한다

• 단순 신경망 모델이나 로지스틱 회귀는 다중클래스 분류 문제를 해결할 수 없지만 활성화 함수로 계단 함수를 시그모이드 함수로 바꾸면 출력값을 확률로 만들 수 있기 때문에 시그모이드 함수를 약간 변형하면 다중클래스 분류 문제를 해결하는데 사용 가능

• 소프트맥스 함수(softmax funcation)는 $n$차원 벡터 $\mathbb{x}=(x_1,x_2,\ldots,x_n)$에 대하여 식 (5.1)로 정의한다
  

\begin{eqnarray} \textrm{softmax}(\mathbb{x})_i=\frac{e^{\mathbb{x}_i}}{\sum_{j=1}^ne^{\mathbb{x}_j}}\quad(i=1, 2, \ldots, n)\tag{5.1}\end{eqnarray}

• $y_i= \textrm{softmax}(\mathbb{x})_i$를 성분으로 갖는 벡터를 $\mathbb{y}$라고 하면 소프트맥스 함수의 정의로 부터 식 (5.2)가 성립

\begin{align} \sum_{i=1}^ny_i &= \sum_{i=1}^n \frac{e^{\mathbb{x}_i}}{\sum_{j=1}^ne^{\mathbb{x}_j}} \quad(0\leqq y_i \leqq 1\,\,(i=1,2,\ldots,n))\\ &= \frac{\sum_{i=1}^ne^{\mathbb{x}_i}}{\sum_{j=1}^ne^{\mathbb{x}_j}}\\&= 1\tag{5.2}\end{align}

• 각각의 성분 표시를 일반화하면 식 (5.3)으로 표현 가능하기 때문에 $y_i$는 식 (5.4)가 된다
  

\begin{eqnarray} \mathbb{y} = \left( \begin{array}{c}y_1\\y_2\\\vdots\\y_n\end{array}\right) = \frac{1}{\sum_{j=1}^ne^{x_j}}\left( \begin{array}{c}e^{x_1}\\e^{x_2}\\\vdots\\e^{x_n}\end{array}\right)\tag{5.3}\end{eqnarray}

\begin{eqnarray} y_i = \frac{e^{x_i}}{\sum_{j=1}^n e^{x_j}}\tag{5.4}\end{eqnarray}

소프트맥스 함수의 예

• $\mathbb{x}=\left(\begin{array}{c}2 & 1 & 1\end{array}\right)$이라면

\begin{align}\mathbb{y} &= \left(\begin{array}{c} y_1& y_2 & y_3\end{array}\right)\\ &= \frac{1}{e^2 + e^1 + e^1}\left(\begin{array}{c} e^2 & e^1 & e^1\end{array}\right) \\ &= \frac{1}{12.8256} \left(\begin{array}{c} 7.3891 & 2.7183 & 2.7183 \end{array}\right)\\ &= \left(\begin{array}{c} 0.5761 & 0.2119 & 0.2119\end{array}\right) \end{align}

소프트맥스 함수의 경사도

• 소프트맥스 함수를 사용하면 출력 벡터의 성분이 정규화되어 '출력 확률'로 취급할 수 있기 때문에 신경망 모델에 사용이 가능

• 소프트맥스 함수의 경사도를 구하기 위해 입력 벡터 $x_i$의 편미분 식을 구하기 위해 식 (5.3) 우변의 분모를 식 (5.5)로 정의

\begin{eqnarray} Z = \sum_{j=1}^n e^{x_j} \tag{5.5}\end{eqnarray}

• 이제 소프트맥스 함수를 $x_i$로 편미분을 해보자

• $i=j$일 때

\begin{align} \frac{\partial y_i}{\partial x_i} &= \frac{e^{x_i}Z - e^{x_i}e^{x_i}}{Z^2}\\ &= \frac{e^{x_i}}{Z}\bigg(\frac{Z}{Z}-\frac{e^{x_i}}{Z}\bigg)\\ &= y_i(1-y_i)\quad(\because\,\,(5.4),\,(5.5)) \tag{5.5}\end{align}

• $i\neq j$일 때

\begin{align} \frac{\partial y_i}{\partial x_j} &= \frac{\not{e^{x_i}Z} - e^{x_i}e^{x_j}}{Z^2}\\ &= -\frac{e^{x_i}}{Z}\frac{e^{x_j}}{Z} \\ &= -y_iy_j\tag{5.6}\end{align}

• 모든 $i$에 대해서 일반화하기 위해 식 (5.5)와 식 (5.6)을 합쳐서 정리하면 식 (5.7)이 된다

\begin{eqnarray} \frac{\partial y_i}{\partial x_j} = \left\{ \begin{array}{lc} y_i(1-y_i) & (i=j) \\ -y_iy_j & (i\neq j)\end{array}\right.\tag{5.7}\end{eqnarray}

다중클래스 신경망 모델링

• 입력 데이터 $(x_1, \ldots,x_m,\ldots, x_M)$를 $K$개의 클래스 $(y_1, y_2, \ldots, y_K)$로 분류하는 신경망을 모델링하려면 출력이 $K$개가 되어야 하기 때문에 아래 그림과 같은 신경망을 모델링해야 한다
  

• 이 때 출력 $y$는 스칼라가 아닌 $K$ 차원의 벡터가 되기 때문에 식 (5.8)로 표현된다
  

\begin{eqnarray} \mathbb{y} = \left( \begin{array}{c} y_i\\\vdots \\ y_k \\ \vdots\\ y_K \end{array}\right) \tag{5.8}\end{eqnarray}

• 출력은 $K$차원의 벡터이지만 기본적인 개념은 이진 분류 모델과 동일하기 때문에 $y_k$에 대응하는 뉴런만 따로 떼서 보면 해당 뉴런의 출력은 식 (5.9)처럼 되며 이는 이진 분류때와 같은 형태가 되는 것을 알 수 있다
  

\begin{align} y_k &= f(w_{k1}x_1 + w_{k2}x_2 + \cdots + w_{kM}x_M + b_k)\\ &= f(\mathbb{w}\mathbb{x} + b_k)\tag{5.9}\end{align}

• $\mathbb{w}_k=\left(\begin{array}{c} w_{k1} & w_{k2} & \cdots & w_{kM}\end{array}\right)$라고 하면 전체 웨이트 $\boldsymbol{W}$는 식 (5.10)과 되며 바이어스 $b$는 식 (5.11)과 같이 표현할 수 있다

\begin{align} \boldsymbol{W} &= \left(\begin{array}{c} \mathbb{w}_{1} \\ \vdots \\ \mathbb{w}_{k} \\ \vdots \\ \mathbb{w}_{K}\end{array}\right) \\ &= \left(\begin{array}{ccccc} w_{11} & \cdots & w_{1n} & \cdots & w_{1M} \\\vdots &\ddots & \vdots & \ddots& \vdots \\w_{k1} & \cdots & w_{kn} & \cdots & w_{kM}\\\vdots &\ddots & \vdots &\ddots & \vdots \\w_{K1} & \cdots & w_{Kn} & \cdots & w_{KM}\\\end{array}\right)\tag{5.10}\\ \mathbb{b} &= \left(\begin{array}{c} b_{1} \\ \vdots \\ b_{k} \\ \vdots \\ b_{K}\end{array}\right) \tag{5.11}\end{align}

• 식 (5.10)과 식 (5.11)을 사용하여 다중클래스 신경망 모델의 식은 식 (5.12), 그리고 신경망 모델링 가설식은 식 (5.13)으로 나타낼 수 있다

\begin{eqnarray} y = f(\boldsymbol{W}\mathbb{x} + \mathbb{b})\tag{5.12}\end{eqnarray}

\begin{eqnarray} H(\mathbb{x}) = f(\boldsymbol{W}\mathbb{x} + \mathbb{b})\tag{5.12}\end{eqnarray}

• $\boldsymbol{W}$를 웨이트 행렬(weight matrix)라 하고, $\mathbb{b}$를 바이어스 벡터(bias vector)라고 한다
• 발화를 결정하는 활성화 함수 $f(\cdot)$에 소프트맥스 함수를 사용하면 $y$가 식 (5.2)를 만족하기 때문에 다중클래스 분류를 위한 함수로 사용 가능하며 이 모델을 다중클래스 회귀(multi-class logistic regression)라고 한다
  

입력 데이터가 각 클래스로 분류될 확률

• 입력 $\mathbb{x}$가 어떤 클래스로 분류될 확률 변수를 $C$라고 하면

• 이진 분류의 경우: $C\in \{0, 1\}$
• 다중클래스 분류의 경우: $C\in\{1, 2, \ldots, K\}$
  

• 어떤 뉴런의 출력 $y_k$는 $\mathbb{x}$가 클래스 $k$로 분류될 확률이기 때문에 식 (5.14)와 같이 확률식으로 표현 가능

\begin{align} y_k &= \mathrm{Pr}(C=k|\mathbb{x})\\ &=\frac{e^{\mathbb{w}_k\mathbb{x} + b_k}}{\sum_{j=1}^Ke^{\mathbb{w}_j\mathbb{x} + b_j}}\tag{5.14}\end{align}

매개변수 $\boldsymbol{W}$와 $\mathbb{b}$의 가능도 함수

• 실제의 값과 모델의 가설식의 오차를 계산하면서 매개변수 $\boldsymbol{W}$와 $\mathbb{b}$를 업데이트하기 위한 가능도 함수를 구하기 위해 입력 데이터 $\mathbb{x}_n$ $(n=1, 2, \ldots, N)$과 그에 대응하는 정답 데이터 $\mathbb{y}_n$이 있다고 하자

• $\mathbb{x}_n$이 클래스 $k$에 속한다면 식 (5.15)와 같이 $\mathbb{y}_n$의 $k$번째 성분 $\mathbb{y}_{n_k}$는 $1$이지만 그 외의 $j$번째 성분인 $\mathbb{y}_{n_j}$는$0$이 될 것이다

\begin{eqnarray} \mathbb{y}_{n_{j}} = \left\{\begin{array}{lc} 1 & (j = k) \\ 0 & (j\neq k)\end{array}\right.\tag{5.15}\end{eqnarray}

• 식 (5.15)처럼 벡터의 어느 성분만 $1$이고 나머지 성분은 $0$이 되도록 표현하는 것을 $1$-of-$K$ 표현(1-of-K representation)이라고 하며, 식 (5.15)를 코드로 구현하는 것을 원-핫 인코딩(one-hot encoding)이라고 한다

• 다중클래스 모델링 가설식인 식 (5.12)에서 $f(\cdot)=\textrm{softmax}(\cdot)$이라고 하면 $\boldsymbol{W}$와 $\mathbb{b}$의 가장 좋은 값을 찾기 위한 가능도 함수는 식 (5.16)으로 표현할 수 있다

• 각각의 $\mathbb{x}_n$에 대하여 신경망 모델의 출력값이 $\mathbb{y}_{n_k}$가 될 확률 $\mathrm{Pr}(C=k|\mathbb{x}_n)$이 높아야 좋은 모델이다

\begin{align}L(\boldsymbol{W},\mathbb{b}) &= \prod_{n=1}^N\prod_{k=1}^K\mathrm{Pr}(C=k|\mathbb{x}_n)^{\mathbb{y}_{n_k}}\\ &= \prod_{n=1}^N\prod_{k=1}^K\big(H_{n_k}(\mathbb{x}_n)\big)^{\mathbb{y}_{n_k}}\tag{5.16}\end{align}

• 식 (5.16)을 최대로 만드는 매개변수 $\boldsymbol{W}$와 $\mathbb{b}$를 구하기 위해 식 (5.16)에 $\log$를 취하는 변형을 하면 식 (5.17)이 된다

\begin{align} E(\boldsymbol{W}, \mathbb{b}) &= -\log L(\boldsymbol{W},\mathbb{b}) \\ &= -\sum_{n=1}^N\sum_{k=1}^K \mathbb{y}_{n_k}\log H_{n_k}(\mathbb{x}_n)\tag{5.17}\end{align}

• 식 (5.17)을 다중클래스에서의 교차 엔트로피 오차 함수라고 하며, 우리는 이 식의 최적화 문제를 풀어야만 한다

• 최적화 문제를 풀기 위하여 우리는 앞에서 했던 것처럼 경사하강법을 사용해 식 (5.17)의 최소값을 구할 수 있다
  

다중클래스 회귀 모델의 경사하강법

• 웨이트 행렬 $\boldsymbol{W}$의 경사인 편미분 구하기

• $\boldsymbol{W} = (\mathbb{w}_1, \mathbb{w}_2, \ldots, \mathbb{w}_K)$이기 때문에 교차 엔트로피 오차 함수를 식 (5.18)이라 할 수 있다

\begin{align} E &= E(\boldsymbol{W}, \mathbb{b})\\ &= E(\mathbb{w}_1, \mathbb{w}_2, \ldots, \mathbb{w}_K, \mathbb{b})\tag{5.18}\end{align}

• $\boldsymbol{W}$의 $j$번째 성분인 $\mathbb{w}_j$의 편미분 구하기

• $I$를 $K$차 단위행렬, 그리고 $\mathbb{a}_n=\boldsymbol{W}\mathbb{x}_n+\mathbb{b}$라고 하면 식 (5.19)를 구할 수 있다

\begin{align}\frac{\partial E}{\partial \mathbb{w}_j} &= - \sum_{n=1}^N\sum_{k=1}^K\frac{\partial E}{\partial H_{n_k}(\mathbb{x}_n)}\frac{\partial H_{n_k}(\mathbb{x}_n)}{\partial \mathbb{a}_{n_j}} \frac{\partial \mathbb{a}_{n_j}}{\partial \mathbb{w}_j}\\&=-\sum_{n=1}^N\sum_{k=1}^K \frac{\partial}{\partial H_{n_k}(\mathbb{x}_n)}\big(\mathbb{y}_{n_k}\log H_{n_k}(\mathbb{x}_n)\big)\frac{\partial H_{n_k}(\mathbb{x}_n)}{\partial \mathbb{a}_{n_j}} \frac{\partial \mathbb{a}_{n_j}}{\partial \mathbb{w}_j}\\&= -\sum_{n=1}^N\sum_{k=1}^K\frac{\mathbb{y}_{n_k}}{H_{n_k}(\mathbb{x}_n)} \frac{\partial H_{n_k}(\mathbb{x}_n)}{\mathbb{a}_{n_j}}\mathbb{x}_n\\ &= -\sum_{n=1}^N \sum_{k=1}^K \frac{\mathbb{y}_{n_k}}{H_{n_k}(\mathbb{x}_n)}H_{n_k}(\mathbb{x}_n) (I_{k_j}- H_{n_k}(\mathbb{x}_n))\quad(\because\,\,H_{n_k}(\mathbb{x}_n)\,\,\textrm{is softmax})\\ &= -\sum_{n=1}^N\Bigg( \sum_{k=1}^K \mathbb{y}_{n_k}I_{k_j} - \sum_{k=1}^K \mathbb{y}_{n_k}H_{n_j}(\mathbb{x}_n)\Bigg)\mathbb{x}_n\\&= -\sum_{n=1}^N\big(\mathbb{y}_{n_j} - H_{n_j}(\mathbb{x}_n)\big)\mathbb{x}_n\quad(\because\,\,(5.15))\tag{5.19}\end{align}

• $\mathbb{b}$의 $j$번째 성분인 $b_j$의 편미분은 식 (5.20)와 같다
  

\begin{align}\frac{\partial E}{\partial b_j} &= \sum_{n=1}^N\sum_{k=1}^K\frac{\partial E}{\partial H_{n_k}(\mathbb{x}_n)}\frac{\partial H_{n_k}(\mathbb{x}_n)}{\partial \mathbb{a}_{n_j}} \frac{\partial \mathbb{a}_{n_j}}{\partial b_j}\\&=-\sum_{n=1}^N\sum_{k=1}^K \frac{\partial}{\partial H_{n_k}(\mathbb{x}_n)}\big(\mathbb{y}_{n_k}\log H_{n_k}(\mathbb{x}_n)\big)\frac{\partial H_{n_k}(\mathbb{x}_n)}{\partial \mathbb{a}_{n_j}} \frac{\partial \mathbb{a}_{n_j}}{\partial b_j}\\&= -\sum_{n=1}^N\sum_{k=1}^K\frac{\mathbb{y}_{n_k}}{H_{n_k}(\mathbb{x}_n)} \frac{\partial H_{n_k}(\mathbb{x}_n)}{\mathbb{a}_{n_j}}\\ &= -\sum_{n=1}^N \sum_{k=1}^K \frac{\mathbb{y}_{n_k}}{H_{n_k}(\mathbb{x}_n)}H_{n_k}(\mathbb{x}_n) (I_{k_j}- H_{n_k})\quad(\because\,\,H_{n_k}(\mathbb{x}_n))\,\,\textrm{is softmax})\\ &= -\sum_{n=1}^N\Bigg( \sum_{k=1}^K \mathbb{y}_{n_k}I_{k_j} - \sum_{k=1}^K \mathbb{y}_{n_k}H_{n_j}(\mathbb{x}_n)\Bigg)\\&= -\sum_{n=1}^N\big(\mathbb{y}_{n_j} - H_{n_j}(\mathbb{x}_n)\big)\quad(\because\,\,(5.15))\tag{5.20}\end{align}

• 전체 웨이트 행렬 $\boldsymbol{W}$와 바이어스 벡터 $\mathbb{b}$에 대한 편미분 식은 각각의 $j$번째 성분에 대한 편미분이 식 (5.19)와 식 (5.20)이기 때문에 각각의 성분을 모아 벡터로 묶으면 식 (5.21)과 식 (5.22)로 표현할 수 있다

\begin{align} \frac{\partial E}{\partial \boldsymbol{W}} &= -\sum_{n=1}^N \big(\mathbb{y}_n - H_n(\mathbb{x}_n)\big)\mathbb{x}_n\tag{5.21}\\ \frac{\partial E}{\partial \mathbb{b}} &= -\sum_{n=1}^N \big(\mathbb{y}_n - H_n(\mathbb{x}_n)\big)\tag{5.22}\end{align}

TensorFlow로 구현

• 2개의 입력을 받아 3개의 클래스로 분류하기
  

• 각 클래스의 데이터는 평균 $\mu \neq 0$인 정규분포를 따르는 샘플 데이터를 생성해 사용

• 전체 데이터는 300개로 3개의 클래스는 각각 100개의 데이터로 구성되어 있어, 100개를 제대로 분류해야 한다

• 미니배치 확률 경사하강법(SGD)을 사용하려는데, SGD를 사용하기 위해서는 데이터를 무작위로 섞는 작업이 필요하다

• sklearn 라이브러리의 sklearn.utils.shuffle 함수를 사용
  

import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf

M = 2       # 입력 데이터의 차원
K = 3       # 출력 클래스의 수
n = 100     # 각 클래스에 속한 데이터 수
N = n * K   # 전체 데이터 수

# 샘플 데이터 생성
X1 = np.random.randn(n, M) + np.array([0, 10])  # 평균이 [0, 10]인 클래스
X2 = np.random.randn(n, M) + np.array([5, 5])   # 평균이 [5, 5]인 클래스
X3 = np.random.randn(n, M) + np.array([10, 0])  # 평균이 [10, 0]인 클래스

Y1 = np.array([[1, 0, 0] for _ in range(100)])
Y2 = np.array([[0, 1, 0] for _ in range(100)])
Y3 = np.array([[0, 0, 1] for _ in range(100)])

X = np.concatenate((X1, X2, X3), axis=0)
Y = np.concatenate((Y1, Y2, Y3), axis=0)

plt.scatter(X1[:, 0], X1[:, 1], marker='x', label='Class 1')
plt.scatter(X2[:, 0], X2[:, 1], marker='o', label='Class 2')
plt.scatter(X3[:, 0], X3[:, 1], marker='^', label='Class 3')
plt.grid(linestyle=':')
plt.legend()
plt.show()

W = tf.Variable(tf.zeros([M, K]))
b = tf.Variable(tf.zeros([K]))

x = tf.placeholder(tf.float32, shape=[None, M])
y = tf.placeholder(tf.float32, shape=[None, K])

hypothesis = tf.nn.softmax(tf.matmul(x, W) + b)

# 오차 함수는 미니배치로 계산을 하기때문에 각 미니배치의 평균값으로 오차를 계산
cost = tf.reduce_mean(-tf.reduce_sum(y * tf.log(hypothesis), reduction_indices=[1]))

train = tf.train.GradientDescentOptimizer(learning_rate=0.1).minimize(cost)

# 제대로 분류되는지 확인
correct_prediction = tf.equal(tf.argmax(hypothesis, 1), tf.argmax(y, 1))

batch_size = 50
n_batches = N // batch_size

# SGD에서는 각 에포크마다 데이터를 섞는다

with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())

    for epoch in range(20):

        X_, Y_ = shuffle(X, Y)

        for i in range(n_batches):
            start = i * batch_size
            end = start + batch_size

            sess.run(train, feed_dict={x: X_[start:end], y: Y_[start:end]})

    X_, Y_ = shuffle(X, Y)

    classified = correct_prediction.eval(session=sess, feed_dict={x: X_[0:10], y: Y_[0:10]})
    prob = hypothesis.eval(session=sess, feed_dict={x: X_[0:10]})

    print(f'분류 결과: {classified}')
    print()
    print(f'출력 결과 확률:\n{prob}')

• 실행 결과
  

분류 결과: [ True  True  True  True  True  True  True  True  True  True]

출력 결과 확률:
[[9.17210460e-01 8.27893838e-02 7.92326063e-08]
 [9.02648142e-04 9.82177138e-01 1.69202797e-02]
 [2.44496441e-08 2.24424489e-02 9.77557540e-01]
 [9.97427881e-01 2.57207383e-03 3.72525255e-09]
 [9.80204523e-01 1.97954960e-02 7.34132088e-09]
 [1.45240305e-02 9.82932091e-01 2.54384498e-03]
 [9.65797622e-03 8.52199674e-01 1.38142347e-01]
 [5.00551378e-03 9.84985948e-01 1.00085456e-02]
 [9.97002780e-01 2.99719279e-03 1.52783930e-09]
 [9.28733170e-01 7.12668002e-02 4.98736341e-08]]

• 분류 결과를 그래프로 표시

    W = sess.run(W)
    b = sess.run(b)

    print(f'weight matrix: \n{W}')
    print()
    print(f'bias vector: \n{b}')

    plt.scatter(X1[:, 0], X1[:, 1], marker='x', label='Class 1')
    plt.scatter(X2[:, 0], X2[:, 1], marker='o', label='Class 2')
    plt.scatter(X3[:, 0], X3[:, 1], marker='^', label='Class 3')
    plt.grid(linestyle=':')
    plt.legend()

    x_space = np.linspace(-3, 14, 100000)
    plt.plot(x_space, (W[0, 1] - W[0, 0]) / (W[1, 0] - W[1, 1]) * x_space + (b[1] - b[0]) / (W[1, 0] - W[1, 1]))
    plt.plot(x_space, (W[0, 2] - W[0, 1]) / (W[1, 1] - W[1, 2]) * x_space + (b[2] - b[1]) / (W[1, 1] - W[1, 2]))
    plt.show()

weight matrix: 
[[-1.0804898   0.30662853  0.7738616 ]
 [ 0.79061     0.3192574  -1.1098676 ]]

bias vector: 
[-0.05789646  0.10934979 -0.05145331]
 

• 입력 데이터가 2차원이기 때문에 분류의 기준이 되는 직선을 그릴 수 있는데, 소프트맥스 함수의 값이 같아지는 곳이 경계가 된다

• 클래스 1과 클래스 2를 분류하는 직선 : $w_{11}x_1 + w_{12}x_2 + b_1 = w_{21}x_1 + w_{22}x_2 + b_2$

• 클래스 2와 클래스 3을 분류하는 직선 : $w_{21}x_1 + w_{22}x_2 + b_2 = w_{31}x_1 + w_{32}x_2 + b_3$

Keras로 구현

from sklearn.utils import shuffle
import numpy as np
from keras.models import Sequential
from keras.layers import Dense, Activation
from keras.optimizers import SGD

M = 2       # 입력 데이터의 차원
K = 3       # 출력 클래스의 수
n = 100     # 각 클래스에 속한 데이터 수
N = n * K   # 전체 데이터 수

# 샘플 데이터 생성
X1 = np.random.randn(n, M) + np.array([0, 10])  # 평균이 [0, 10]인 클래스
X2 = np.random.randn(n, M) + np.array([5, 5])   # 평균이 [5, 5]인 클래스
X3 = np.random.randn(n, M) + np.array([10, 0])  # 평균이 [10, 0]인 클래스

Y1 = np.array([[1, 0, 0] for _ in range(100)])
Y2 = np.array([[0, 1, 0] for _ in range(100)])
Y3 = np.array([[0, 0, 1] for _ in range(100)])

X = np.concatenate((X1, X2, X3), axis=0)
Y = np.concatenate((Y1, Y2, Y3), axis=0)

model = Sequential()
model.add(Dense(input_dim=M, units=K))
model.add(Activation('softmax'))

# 이진 분류는 loss='binary_crossentropy'
# one-hot encoding은 loss=categorical_crossentropy'
model.compile(loss='categorical_crossentropy', optimizer=SGD(lr=0.1))

minibatch_size = 50

model.fit(X, Y, epochs=20, batch_size=minibatch_size)

X_, Y_ = shuffle(X, Y)
classes = model.predict_classes(X_[0:10], batch_size=minibatch_size)
prob = model.predict_proba(X_[0:10], batch_size=minibatch_size)

print()
print('예측 결과:')
print(np.argmax(model.predict(X_[0:10]), axis=1) == classes)
print()
print(f'출력 확률:\n{prob}')

• 실행 결과
  

예측 결과:
[ True  True  True  True  True  True  True  True  True  True]

출력 확률:
[[9.8160446e-01 1.8395502e-02 5.8491527e-09]
 [9.9367309e-01 6.3269795e-03 1.2570837e-08]
 [2.1171716e-07 5.1151857e-02 9.4884795e-01]
 [9.9820423e-01 1.7957645e-03 1.4402781e-09]
 [5.6637567e-10 4.2483290e-03 9.9575162e-01]
 [6.7489594e-03 9.6715742e-01 2.6093608e-02]
 [1.7853441e-09 5.5074170e-03 9.9449265e-01]
 [2.2595707e-02 9.3311501e-01 4.4289291e-02]
 [6.5676443e-02 9.2871374e-01 5.6097610e-03]
 [8.7217444e-08 1.4764958e-02 9.8523498e-01]]

출처 : 정석으로 배우는 딥러닝

로지스틱 회귀(Logistic Regression)

시그모이드 함수(sigmoid function)

• 퍼셉트론 모델에서 뉴런이 발화하는지($1$) 발화하지 않는지($0$)는 계단함수를 가지고 판별하여 이진 분류(binary classification)를 할 수 있다

• 일상적인 문제에서는 이진분류로만 해결할 수 없는 일들이 많다. 예를 들어 $0$과 $1$이 아닌 어중간한 것들을 판별해야하는 일들이 많다

•  이런 경우에는 $0$과 $1$ 사이의 값에 대응시켜야 하는데, 이런 경우 확률로 대응시킬 수 있어 몇 %의 확률로 예측이 가능하다고 할 수 있다

• 확률을 출력하기 위해서서는 $0$과 $1$ 사이의 실수에 대응시켜줄 수 있는 함수가 필요한데 이런 성질을 만족하는 함수 중의 하나가 식 (4.1)이며 시그모이드 함수(sigmoid function) 또는 로지스틱 함수(logistic function)이라고 한다

\begin{eqnarray} \sigma(x) = \frac{1}{1+e^{-x}}\tag{4.1}\end{eqnarray}

• 계단함수와 시그모이드 함수의 비교

시그모이드 함수와 확률 밀도 함수, 누적 분포 함수와의 관계

• 확률 밀도 함수(PDF; Probability Density Function) : 확률 변수의 분포를 나타내는 함수로 확률 변수 $X$가 $a$ 이상 $b$ 이하가 될 확률을 식 (4.2)와 같이 표현할 때 $f(x)$를 확률밀도함수라고 한다
  

\begin{eqnarray}\textrm{Pr}(a\leqslant X \leqslant b) = \int_a^b f(x) dx\tag{4.2}\end{eqnarray}

• $f(x)$는 확률이기 때문에 다음 두 조건 식 (4.3)과 식 (4.4)를 만족해야 한다

1. 모든 실수 $x$에 대하여\begin{eqnarray}f(x) \geqslant 0\tag{4.3}\end{eqnarray}
2. 실수 범위를 가지는 확률 변수 $X$에 대하여\begin{eqnarray}\textrm{Pr}(-\infty \leqslant X \leqslant \infty) = \int_{-\infty}^{\infty}f(x)dx=1\tag{4.4}\end{eqnarray}
   

• 누적 분포 함수(CDF; Cumulative Distribution Function) : 어떤 확률 분포에서 확률 변수가 특정값보다 작거나 같은 확률로 실수 범위를 가지는 확률 변수 $X$의 누적 분포 함수를 $F(x)=P(X\leqslant x)$이라고 할 때, 식 (4.5)와 같이 표현된다

\begin{eqnarray}F(x)= \int_{-\infty}^x f(t)dt\tag{4.5}\end{eqnarray}

• 식 (4.2)와 식 (4.5)로부터 확률 밀도 함수와 누적 분포 함수 사이에는 식 (4.6)과 같은 관계가 있는 것을 알 수 있다

\begin{eqnarray} \frac{d}{dx}F(x) = F'(x) = f(x)\tag{4.5}\end{eqnarray}

정규분포의 확률 밀도 함수와 누적 분포 함수

• 확률을 표현하는 함수로는 확률 밀도 함수와 누적 분포 함수가 있는데, 누적 분포 함수는 값이 $0$부터 $1$까지의 범위에 있으므로 함수값이 확률을 나타내는 함수로 적절

• 그러나 특정 값만 취하는 함수를 사용한다면 확률 변수 $x$의 분포에 편향이 생길 수 있기 때문에 확률 변수의 분포가 가장 일반적인 정규분포를 따르는 함수를 생각해보자

• 평균이 $\mu$이고 표준편차가 $\sigma$인 정규분포의 확률 밀도 함수는 식 (4.6)와 같으며, 그림과 같이 정규분포의 누적 분포 함수의 값도 $0$에서 $1$ 사이에 있다
  

\begin{eqnarray} f(x) = \frac{1}{\sqrt{2\pi\sigma}}e^{-\frac{(x-\mu)^2}{2\sigma^2}}\tag{4.6}\end{eqnarray}

import numpy as np
import matplotlib.pyplot as plt

x = np.linspace(-10, 11, 100000)

fig = plt.figure()
ax1 = fig.add_subplot(1, 2, 1)

def pdf(x, mu=0, sigma=1):
    return (np.exp(-(x-mu)**2/2/(sigma**2))) / (np.sqrt(2*math.pi)*sigma)

for sigma in range(1, 4):
    ax1.plot(x, pdf(x, sigma=sigma), label=f'$\sigma$={sigma}')

ax1.legend()
ax1.grid(linestyle=':')
ax1.set_title("PDF of Normal Distribution")
ax1.set_xticks([0])

ax2 = fig.add_subplot(1, 2, 2)

from scipy.special import erf

def cdf(x, mu=0, sigma=1):
    return (1 + erf((x - mu) / np.sqrt(2) / sigma)) / 2

for sigma in range(1, 4):
    ax2.plot(x,cdf(x, sigma=sigma),label=f'$\sigma$={sigma}')

ax2.legend(loc=5)
ax2.grid(linestyle=':')
ax2.set_title('CDF of Normal Distribution')
ax2.set_xticks([0])
ax2.set_yticks([0, 1])
plt.show()

• 로지스틱 회귀는 활성화 함수로 시그모이드 함수를 사용하는데, 시그모이드 함수 대신 정규분포의 누적 분포 함수를 사용하는 모델을 프로빗 회귀(probit regression)이라고 한다

• 정규분포의 확률 누적 함수가 확률을 출력하는 함수로 시그모이드 함수보다 더 적절하지만 신경망 모델에서는 거의 사용되지 않음

정규분포의 확률 누적 분포 함수가 사용되지 않는 이유

• 표준정규분포의 누적 분포 함수 $p(x)$를 이용해 뉴런을 모델화하는 것을 생각해보면 가설 모델은 식 (4.7)과 같이 표현할 수 있다

\begin{align} H(\mathbb{x}) & = \textrm{Pr}(\mathbb{wx} + b) \\ & = \int_{-\infty}^{\mathbb{wx}+b}\frac{1}{\sqrt{2\pi}}e^{-\frac{(\mathbb{w}t+b)^2}{2}}dt\tag{4.7}\end{align}

• 학습을 위해서는 실제의 값과 뉴런 모델의 출력값의 차가 최소가 되도록 웨이트와 바이어스를 조절해야하는데, 식 (4.7)를 사용하는 경우에는 이를 계산하는 것이 쉬운 일이 아니다

• 오차가 최소가 되도록 매개변수의 값을 업데이트하는 것이 쉬워야하기 때문에 다소 오차는 있지만 누적 분포 함수와 모양의 거의 흡사하면서도 계산은 매우 쉬운 시그모이드 함수를 사용하는 것이 편리하다. 아래 그림은 $\sigma=1$과 $\sigma=2$일 때의 누적 분포 함수와 시그모이드 함수의 그래프를 비교한 것이다

• 모든 일에서 이론도 매우 중요하지만 '현실적으로 계산이 가능한가?'라는 생각을 가지고 공학적으로 접근한 것도 중요하다
  

import numpy as np
import matplotlib.pyplot as plt
from scipy.special import erf

x = np.linspace(-10, 11, 100000)

def sigmoid(x):
    return 1 / (1+np.exp(-x))

def cdf(x, mu=0, sigma=1):
    return (1 + erf((x - mu) / np.sqrt(2) / sigma)) / 2

plt.plot(x, sigmoid(x), label='sigmoid function')
plt.plot(x, cdf(x, sigma=1), label='CDF where $\sigma$=1')
plt.plot(x, cdf(x, sigma=2), label='CDF where $\sigma$=2')
plt.grid(linestyle=":")
plt.xticks([0])
plt.yticks([0, 1])
plt.legend()
plt.show()

로지스틱 회귀 모델화

• 로지스틱 회귀는 단순 퍼셉트론과는 달리 $0$과 $1$ 사이의 값을 갖는 확률적인 분류 모델이기 때문에 단순 신경망 모델과는 다른 모델링 방법을 사용해야 한다

• 어떤 입력 $x$에 대하여 뉴런이 발화할지 여부를 나타내는 확률변수를 $C$라고 하면 $C$는 뉴런이 발화할 경우 $C=1$이 되고 발화하지 않을 경우 $C=0$이 되는 확률변수이기 때문에 단순 신경망 모델식을 고려해보면 뉴런이 발화할 확률은 식 (4.8)과 같다

\begin{eqnarray} \textrm{Pr}(C=1|x)=\sigma(\mathbb{wx}+b)\tag{4.8}\end{eqnarray}

• 뉴런이 발화하는 않을 확률은 식 (4.9)와 같다
• 뉴런이 발화하거나 발화하지 않은 확률은 둘 중의 하나이기 때문에 $1$이다

\begin{eqnarray} \textrm{Pr}(C=0|x) = 1 - \textrm{Pr}(C=1|x)\tag{4.9}\end{eqnarray}

• $C$는 $1$(발화)이거나 $0$(발화하지 않음)의 두 가지 값만 갖기 때문에 가설 모델을 $H(\mathbb{x})=\sigma(\mathbb{wx}+b)$라고 하면, $y\in\{0,1\}$일 때 식 (4.8)과 식 (4.9)는 식 (4.10)으로 표현할 수 있다

\begin{eqnarray} \textrm{Pr}(C=y|x)=(H(\mathbb{x}))^y(1-H(\mathbb{x}))^{1-y} \tag{4.10}\end{eqnarray}

• $y=0$인 경우, 

\begin{align}\textrm{Pr}(C=0|x) &=(H(\mathbb{x}))^0(1-H(\mathbb{x}))^{1-0}\\&=1\cdot(1-H(\mathbb{x}))^1\\&=1-H(\mathbb{x})\\&=1-\sigma(\mathbb{wx}+b)\\&=1-\textrm{Pr}(C=1|x)\end{align}

• $y=1$인 경우,
  

\begin{align}\textrm{Pr}(C=1|x)&=(H(\mathbb{x}))^1(1-H(\mathbb{x}))^{1-1}\\ &=y\cdot(1-H(\mathbb{x}))^0\\ &=y\cdot 1\\ &=H(\mathbb{x})\\ &=\sigma(\mathbb{wx}+b)\\ &=\textrm{Pr}(C=1|x)\end{align}

• $N$개의 입력 데이터 $\mathbb{x}_n(n=1, 2,\ldots,N)$과 이 입력 데이터와 쌍을 이루는 출력 데이터 $\mathbb{y}_n$이 주어졌을 때 신경망의 매개변수인 $\mathbb{w}$와 바이어스 $b$의 가장 좋은 값을 찾기 위하여 가능도 또는 우도 함수(likelihood function)는 표준정규분포의 누적 분포 함수 대신에 시그모이드 함수를 사용한 가설식 (4.11)를 사용해 식 (4.12)과 같이 나타낼 수 있다

 \begin{eqnarray} H(\mathbb{x})=\sigma(\mathbb{wx}+b) \tag{4.11}\end{eqnarray}

• 각각의 $\mathbb{x}_n$에 대하여 신경망 모델의 출력값이 $\mathbb{y}_n$이 될 확률 $\textrm{Pr}(C=\mathbb{y}_n|\mathbb{x}_n)$이 높아야 좋은 모델이다
  

\begin{align} L(\mathbb{w},b) &= \prod_{n=1}^{N}\textrm{Pr}(C=\mathbb{y}_n|\mathbb{x}_n)\\ &= \prod_{n=1}^{N} (H_n(\mathbb{x}))^{\mathbb{y}_n}(1-H_n(\mathbb{x}))^{1-\mathbb{y}_n}\tag{4.12}\end{align}

• 식 (4.12)의 가능도 함수 또는 우도 함수의 값이 최대가 되도록 매개변수를 업데이트하면 신경망 모델이 학습을 잘한 것이라고 볼 수 있다

• 함수의 최대나 최소가 되는 상태를 구하는 문제를 최적화 문제(optimization problem)라고 한다
• 함수의 최대화는 부호를 바꾸면 최소화가 되기 때문에 일반적으로 함수를 최적화한다고 하는 것은 함수를 최소로 만드는 매개변수를 구하는 것을 의미한다

함수 최적화와 미분 관계

• 함수 최적화 문제는 함수를 최대나 최소로 만드는 매개변수를 구하는 것이기 때문에 함수의 최대와 최소는 미분(differentiation)과 관계가 있기 때문에 우리는 식 (4.12)를 매개변수들로 편미분(partial differentiation)하는 문제를 생각해야 한다

• 식 (4.12)는 함수가 곱의 형태로 되어 있어 편미분을 계산하는 것이 쉽지 않기 때문에 편미분 계산이 쉽도록 식 (4.11)에 로그를 취해 덧셈 형태로 변환하고 최소가 되는 최적화 문제가 되도록 음수의 형태로 변환하면 식 (4.13)이 된다

\begin{align} E(\mathbb{w}, b) &= -\log L(\mathbb{w}, b)\\ &= -\log \prod_{n=1}^{N} (H_n(\mathbb{x}))^{\mathbb{y}_n}(1-H_n(\mathbb{x}))^{1-\mathbb{y}_n}\\&= -\sum_{n=1}^N\Big(\mathbb{y}_n\log H_n(\mathbb{x})+(1-\mathbb{y}_n)\log (1-H_n(\mathbb{x})\Big)\tag{4.13}\end{align}

• 식 (4.13)과 같은 형태의 함수를 교차 엔트로피 오차 함수(cross-entropy error fuction 또는 crosss-entropy cost function)이라고 하며, 이 함수를 최소화하는 것이 식 (4.12) 가능도 또는 우도 함수를 최대화하는 것이기 때문에 식 (4.12)는 최적의 상태에서 오차가 어느 정도 있는지를 알 수 있는 식이라고 할 수 있기 때문에 식 (4.13)를 오차 함수(cost function) 또는 손실 함수(loss function)이라고 한다
  

경사하강법

• 식 (4.13) 오차 함수에서 매개변수는 $\mathbb{w}$와 $b$이기  때문에 $\mathbb{w}$와 $b$로 편미분해서 $0$이 되는 값이 오차 함수가 최소가 되기 때문에 이 식을 직접 해석적으로 식을 풀어 해를 구하는 것은 쉬운 문제가 아니다

• 해석적으로 식을 푸는 방법보다는 단순 신경망 모델에서 처럼 오차를 계산하여 줄여나가는 방법으로 매개변수를 갱신하는 방법을 사용해야 하는데 매개변수를 업데이트하며 오차를 최소하는 방법 중 대표적인 것이 경사하강법(GDA; Gradient Descent Algorithm)이다

• 가중치 $\mathbb{w}$와 바이어스 $b$는 식 (3.9)와 식 (3.10)과 같은 방법으로 업데이트된다
  

\begin{align}\mathbb{w}^{k+1} &=\mathbb{w}^k + \Delta\mathbb{w}^k \tag{3.9} \end{align}

\begin{align} b^{k+1} &= b^k + \Delta b^k\tag{3.10}\end{align}

• 경사하강법에서 가중치와 바이어스는 식 (4.14)와 식 (4.15)와 같은 방법으로 계산

• $\alpha(>0)$는 학습률(learning rate)이라는 하이퍼파라미터(hyperparameter)로 알고리즘 내부 설정값인데 이는 가설 모델의 매개변수가 업데이트 또는 최소로 수렴하는 정도를 조절하는 매개변수
• 보통 $0.1$이나 $0.01$과 같은 적당히 작은 값을 사용
  

\begin{align} \mathbb{w}^{k+1} &= \mathbb{w}^k - \alpha \frac{\partial E(\mathbb{w},b)}{\partial \mathbb{w}} \tag{4.14}\end{align}

\begin{align} b^{k+1} &= b^k-\alpha \frac{\partial E(\mathbb{w}, b)}{\partial b} \tag{4.15}\end{align}

• 가중치 $\mathbb{w}$에 대한 기울기를 편미분을 통해 구하기 위해 $n$번째 오차 함수 $E_n$을 식 (4.16)로 정의한다

\begin{eqnarray} E_n = -\big( \mathbb{y}_n \log H_n(\mathbb{x}) + (1-\mathbb{y}_n)\log (1-H_n(\mathbb{x})\big)\tag{4.16}\end{eqnarray}

• 가중치 $\mathbb{w}$에 대한 기울기는 식 (4.17)과 같이 구할 수 있다

\begin{align} \frac{\partial E(\mathbb{w},b)}{\partial \mathbb{w}} &= \sum_{n=1}^N\frac{\partial E_n}{\partial H_n(\mathbb{x})}\frac{\partial H_n(\mathbb{x})}{\partial \mathbb{w}}\\ &= -\sum_{n=1}^N \Bigg(\frac{\mathbb{y}_n}{H_n(\mathbb{x})} - \frac{1-\mathbb{y}_n}{1-H_n(\mathbb{x})}\Bigg) \frac{\partial H_n(\mathbb{x})}{\partial \mathbb{w}}\quad(\because\,\, H(\mathbb{x})=\sigma(\mathbb{wx}+b)\,\,(4.11))\\ &= -\sum_{n=1}^N \Bigg(\frac{\mathbb{y}_n}{H_n(\mathbb{x})} - \frac{1-\mathbb{y}_n}{1-H_n(\mathbb{x})}\Bigg)  H_n(\mathbb{x})(1-H_n(\mathbb{x}))\mathbb{x}_n\quad(\because \,\, (4.18))\\ &= -\sum_{n=1}^N\Big( \mathbb{y}_n(1-H_n(\mathbb{x}))-H_n(\mathbb{x})(1-\mathbb{y}_n)  \Big)\mathbb{x}_n \\ &= -\sum_{n=1}^N\big(\mathbb{y}_n-H_n(\mathbb{x})\big)\mathbb{x}_n\tag{4.17}\end{align}

\begin{align}\frac{d}{dx}\sigma(x) &= \frac{d}{dx}(1+e^{-x})^{-1}\\ &= (-1)(1+e^{-1})^{-1-1}\frac{d}{dx}(1+e^{-x})\\ &= \frac{-1}{(1+e^{-x})^{2}}\bigg(\frac{d}{dx}1+\frac{d}{dx}e^{-x}\bigg) \\ &= \frac{-1}{(1+e^{-x})^{2}}\bigg(0+e^{-x}\frac{d}{dx}(-x)\bigg) \\&=\frac{-1}{(1+e^{-x})^{2}}e^{-x}(-1) \\ &= \frac{e^{-x}}{(1+e^{-2})^2} \\ &=  \frac{1+ e^{-x} -1}{(1+e^{-2})^2}\\ &=\frac{1+e^{-x}}{(1+e^{-x})^2}-\frac{1}{(1+e^{-x})^2}\\&= \frac{1}{1+e^{-x}} -\frac{1}{(1+e^{-x})^2}\\ &= \frac{1}{1+e^{-x}}\bigg(1-\frac{1}{1+e^{-x}}\bigg)\\ &= \sigma(x)(1-\sigma(x)) \tag{4.18}\end{align}

• 바이어스 $b$에 대한 기울기는 식 (4.19)과 같이 구할 수 있다

\begin{align} \frac{\partial E(\mathbb{w},b)}{\partial b} &= \sum_{n=1}^N\frac{\partial E_n}{\partial H_n(\mathbb{x})}\frac{\partial H_n(\mathbb{x})}{\partial b}\\ &= -\sum_{n=1}^N \Bigg(\frac{\mathbb{y}_n}{H_n(\mathbb{x})} - \frac{1-\mathbb{y}_n}{1-H_n(\mathbb{x})}\Bigg) \frac{\partial H_n(\mathbb{x})}{\partial b}\quad(\because\,\, H(\mathbb{x})=\sigma(\mathbb{wx}+b)\,\,(4.11))\\ &= -\sum_{n=1}^N \Bigg(\frac{\mathbb{y}_n}{H_n(\mathbb{x})} - \frac{1-\mathbb{y}_n}{1-H_n(\mathbb{x})}\Bigg)  H_n(\mathbb{x})(1-H_n(\mathbb{x}))\quad(\because \,\, (4.18))\\ &= -\sum_{n=1}^N\Big( \mathbb{y}_n(1-H_n(\mathbb{x}))-H_n(\mathbb{x})(1-\mathbb{y}_n)  \Big) \\ &= -\sum_{n=1}^N\big(\mathbb{y}_n-H_n(\mathbb{x})\big)\tag{4.19}\end{align}

• 경사하강법을 통해 우리가 구하고자 하는 가중치 식 (4.14)와 바이어스 식 (4.15)는 각각 식 (4.20) 및 식 (4.21)과 같이 구할 수 있다

\begin{align} \mathbb{w}^{k+1} &= \mathbb{w}^k - \alpha \frac{\partial E(\mathbb{w},b)}{\partial \mathbb{w}} \\&= \mathbb{w}^k + \alpha\sum_{n=1}^N\big(\mathbb{y}_n-H_n(\mathbb{x})\big)\mathbb{x}_n\tag{4.20}\end{align}

\begin{align} b^{k+1} &= b^k-\alpha \frac{\partial E(\mathbb{w}, b)}{\partial b} \\ &= b^k+\alpha\sum_{n=1}^N\big(\mathbb{y}_n-H_n(\mathbb{x})\big)\tag{4.21}\end{align}

확률적 경사하강법과 미니배치 경사하강법

• 식 (4.20)와 식 (4.21)의 경사하강법을 통해 로지스틱 회귀 문제를 해결할 수 있지만 실제 구현에 있어서는 한번 학습을 할 때마다 학습 데이터의 개수만큼 $N$번의 합을 구해야만 하는 문제가 발생하는데, $N$이 작으면 큰 문제가 없지만 $N$이 큰 경우에는 구현상에 문제가 발생

• 메모리에 적재할 때 용량의 문제로 메모리에 다 올려놓지 못하는 경우가 발생하는 문제
• 계산 시간이 증가하는 문제

• 이 문제를 해결하기 위한 대책으로 나오는 것이 확률적 경사하강법(SGD; Stochastic Gradient Descent Algorithm)

• 경사하강법 : 모든 입력데이터의 합을 구한 후 매개변수 업데이트

\begin{align} \mathbb{w}^{k+1} &=  \mathbb{w}^k + \alpha\sum_{n=1}^N\big(\mathbb{y}_n-H_n(\mathbb{x})\big)\mathbb{x}_n\\ b^{k+1} &= b^k+\alpha\sum_{n=1}^N\big(\mathbb{y}_n-H_n(\mathbb{x})\big)\end{align}

• 확률적 경사하강법 : $N$개의 데이터 중에서 무작위로 1개를 선택해 계산 후 매개변수 업데이트
  

\begin{align} \mathbb{w}^{k+1} &= \mathbb{w}^k + \alpha\big(\mathbb{y}_n-H_n(\mathbb{x})\big)\mathbb{x}_n\tag{4.22}\\ b^{k+1} &= b^k+\alpha\big(\mathbb{y}_n-H_n(\mathbb{x})\big)\tag{4.23}\end{align}

• 식 (4.22)와 식 (4.23)을 $N$개의 데이터에 대해 계산
• 장점 : 경사하강법 1번의 계산량으로 확률적 경사하강법을 $N$번 계산할 수 있기 때문에 효율적으로 최적의 해를 찾을 수 있음
• 단점 : 경사가 $0$으로 수렴하는 일이 거의 없기 때문에 최소해를 찾기가 힘들 뿐만 아니라 $N$개의 데이터 전체에 대하여 반복해서 학습을 해야함
  
• 에포크(epoch) : $N$개의 데이터 전체에 대한 반복 학습 횟수
• 각 에포크마다 데이터를 무작위로 섞어서(shuffle) 학습을 하기 때문에 학습을 할 때 편향되지 않은 최적의 해를 찾기 쉬워짐

for epoch in range(epochs):
    shuffle(data)       # 에포크마다 데이터를 섞는다
    for datum in data:  # 데이터를 1개씩 사용해 매개변수를 업데이트한다
        parameters_gradient = evaluate_gradient(cost_function, parameters, datum)
        parameters -= learning_rate * parameters_gradient 

• 미니배치 경사하강법(Minibatch Gradient Descent Algorithm) : 경사하강법과 확률적 경사하강법의 중간에 위치한 방법으로 $N$개의 데이터를 $M(\leqq N)$개씩으로 나눠서(미니배치) 학습하는 방법이며, $M$는 대략 $50 \leqq M \leqq 500$정도의 값을 사용하며, 이와 대비하여 일반 경사하강법을 배치 경사하강법이라고도 한다

• 미니배치 경사하강법을 사용하면 메모리의 부족함없이 선형대수를 사용하여 연산할 수 있기 때문에 1개씩 반복 계산하는 것보다 빠르게 연산이 가능
• 일반적으로 '확률적 경사하강법'이라고 하면 '미니배치 경사하강법'을 말하는데, $M=1$인 경우가 정확한 확률적 경사하강법에 해당함
  

for epoch in range(epochs):
    shuffle(data)           # 에포크마다 데이터를 섞는다
    batches = get_batches(data, batch_size=M)
    for batch in batches:   # 각 미니배치마다 매개변수를 업데이트한다
        parameters_gradient = evaluate_gradient(cost_function, parameters, datum)
        parameters -= learning_rate * parameters_gradient 

OR 게이트 로지스틱 회귀를 TensorFlow로 구현

• 파이썬 코드
  

import numpy as np
import tensorflow as tf

X = np.array([[0, 0],
              [0, 1],
              [1, 0],
              [1, 1]])

Y = np.array([[0],
              [1],
              [1],
              [1]])

W = tf.Variable(tf.zeros([2, 1]))
b = tf.Variable(tf.zeros([1]))

x = tf.placeholder(tf.float32, shape=[None, 2])
y = tf.placeholder(tf.float32, shape=[None, 1])

hypothesis = tf.nn.sigmoid(tf.matmul(x, W) + b)
cost = -tf.reduce_sum(y * tf.log(hypothesis) + (1-y)*tf.log(1-hypothesis))
train = tf.train.GradientDescentOptimizer(learning_rate=0.1).minimize(cost)

correct_predict = tf.equal(tf.to_float(tf.greater(hypothesis, 0.5)), y)

with tf.Session() as sess:
    init = tf.global_variables_initializer()
    sess.run(init)

    for epoch in range(200):
        sess.run(train, feed_dict={x: X, y: Y})

    classified = correct_predict.eval(session=sess, feed_dict={x: X, y: Y}) # OR 게이트 예측값
    print(f'OR 게이트 예측 결과: \n{classified}')

    prob = hypothesis.eval(session=sess, feed_dict={x: X, y: Y})            # OR 게이트의 출력 확률
    print(f'OR 게이트 출력 확률: \n{prob})

• 실행 결과
  

OR 게이트 예측 결과 :
[[ True]
 [ True]
 [ True]
 [ True]]

OR 게이트 출력 확률 :
[[0.22355038]
 [0.9142595 ]
 [0.9142595 ]
 [0.99747425]]

OR 게이트 로지스틱 회귀를 Keras로 구현

• 파이썬 코드

import numpy as np
from keras.models import Sequential
from keras.layers import Dense, Activation
from keras.optimizers import SGD

# 가설식 모델 정의 : 입력(input_dim) 2개, 출력(units) 1개
# 발화를 결정하는 활성화 함수는 누적 분포 함수가 아닌 sigmoid를 사용
model = Sequential()
model.add(Dense(input_dim=2, units=1))
model.add(Activation('sigmoid'))

# 가설식의 오차 함수는 cross-entropy 함수를 사용
model.compile(loss='binary_crossentropy', optimizer=SGD(learning_rate=0.1))

X = np.array([[0, 0],
              [0, 1],
              [1, 0],
              [1, 1]])

Y = np.array([[0],
              [1],
              [1],
              [1]])

# 가설식 모델 학습시키기
model.fit(X, Y, epochs=200, batch_size=1)

# 학습 결과 확인하기
classes = model.predict_classes(X, batch_size=1)
prob = model.predict_proba(X, batch_size=1)

print(f'\nOR 게이트 예측 결과 :\n{Y==classes})')
print()
print(f'OR 게이트 출력값 확률:\n{prob}')

• 실행 결과

1/4 [======>.......................] - ETA: 0s - loss: 0.2746
4/4 [==============================] - 0s 500us/step - loss: 0.1184
Epoch 197/200

1/4 [======>.......................] - ETA: 0s - loss: 0.0911
4/4 [==============================] - 0s 751us/step - loss: 0.1179
Epoch 198/200

1/4 [======>.......................] - ETA: 0s - loss: 0.0031
4/4 [==============================] - 0s 501us/step - loss: 0.1174
Epoch 199/200

1/4 [======>.......................] - ETA: 0s - loss: 0.0905
4/4 [==============================] - 0s 750us/step - loss: 0.1169
Epoch 200/200

1/4 [======>.......................] - ETA: 0s - loss: 0.2696
4/4 [==============================] - 0s 750us/step - loss: 0.1163

OR 게이트 예측 결과 :
[[ True]
 [ True]
 [ True]
 [ True]]

OR 게이트 출력값 확률:
[[0.23539683]
 [0.9141111 ]
 [0.906056  ]
 [0.99700963]]

출처 : 정석으로 배우는 딥러닝

일반 신경망의 모델화

단순 신경망 모델의 일반화

• 입력이 2개였던 단순 신경망 모델을 아래 그림과 같이 입력의 개수를 $n$개로 확장해서 일반화를 시켜보자
  

• 전기신호를 전달하는 뉴런의 수가 늘어나더라도 '받아들은 전기량의 임계값을 넘으면 발화한다'라는 뉴런의 특징은 변하지 않기 때문에 가설 모델  $H(\mathbb{x})$는 식 (3.1)과 같이 표현할 수 있다
  

\begin{eqnarray} H(\mathbb{x}) = \left\{ \begin{array}{ll} 1 & w_1x_1 + w_2x_2 + \cdots + w_nx_n \geqslant \theta \\ 0 & w_1x_1 + w_2x_2 + \cdots + w_nx_n < \theta\end{array}\right. \tag{3.1} \end{eqnarray}

• 식 (3.2)와 같은 함수 $f(x)$가 있다고 가정하면

\begin{eqnarray} f(x) = \left\{ \begin{array}{ll} 1 & x \geqslant 0 \\ 0 & x < 0 \end{array}\right. \tag{3.2} \end{eqnarray}

• 신경망의 출력 $H(\mathbb{x})$는 식 (3.3)과 같이 표현할 수 있으며, 이 때 함수 $f(x)$를 계단함수(step function)라고 한다
  

\begin{align} H(\mathbb{x}) &= f(w_1x_1+x_2x_2+\cdots+w_nx_n-\theta)\\ &= f\Big(\sum_{i=1}^nw_ix_i -\theta\Big)\tag{3.3}\end{align}

• 계산의 편의를 위해서 $b=-\theta$로 바꾸고 가중치 $w_i$와 입력 $x_i$ $(i=1,2,\ldots, n)$를 벡터의 형태로 나타낼 수 있기 때문에 식 (3.4)와 식 (3.5)와 같이 나타낼 수 있다

• 벡터를 사용하면 식이 간단해서 이해하기 쉬울 뿐만 아니라 프로그램 코드로 구현을 할 때에도 벡터를 배열로 대응시키면 직관적으로 구현이 가능
  

\begin{eqnarray} \mathbb{w} = (w_1, w_2, \ldots, w_n)\tag{3.4}\end{eqnarray}

\begin{eqnarray} \mathbb{x} = \left( \begin{array}{c} x_1\\ x_2\\ \vdots\\ x_n\end{array}\right) \tag{3.5}\end{eqnarray}

• 식 (3.4)와 식 (3.5)를 사용하여 식 (3.3)을 변형하면 식 (3.6)과 같이 쓸 수 있는데, 뉴런의 출력을 식 (3.6)과 같이 표현한 신경망 모델을 퍼셉트론(perceptron)이라고 하며 단순 신경망 모델을 단순 퍼셉트론(simple perceptron)이라고 한다. 식 (3.6)에서 벡터 $\mathbb{w}$를 웨이트 벡터(weight vector)라고 하며, $b$를 편향 또는 바이어스(bias)라고 한다
  

\begin{eqnarray} H(\mathbb{x}) = f(\mathbb{wx}+b)\tag{3.6}\end{eqnarray}

• 단순 퍼셉트론을 모델화할 때 매개변수 $(w_1, w_2, \theta)$의 값을 조절하는 오차정정학습법을 사용하였다면 퍼셉트론을 모델화할 때에는 웨이트 벡터 $\mathbb{w}$와 바이어스 $b$를 조절하면서 오차정정학습법을 사용해야 하기 때문에 오차정정을 위한 차는 단순 퍼셉트론의 경우처럼 식 (3.7)~식 (3.10)과 같이 정리할 수 있다

\begin{align} \Delta\mathbb{w} & = (y-H(\mathbb{x}))\mathbb{x} \tag{3.7}\\ \Delta b &=y-H(\mathbb{x})\tag{3.8}\\ \mathbb{w}^{k+1} &=\mathbb{w}^k + \Delta\mathbb{w}^k \tag{3.9} \\ b^{k+1} &= b^k + \Delta b^k\tag{3.10}\end{align}

퍼셉트론 구현

• 두 종류의 정규분포를 따르는 데이터를 분류하는 퍼셉트론 모델을 만들어보자
  

• 뉴런이 발화하지 않는 데이터의 평균값은 $0$이고, 뉴런이 발화하는 데이터의 평균값은 $5$이며 각각 10개의 데이터를 생성하는 코드는 다음과 같다
  

import numpy as np
import matplotlib.pyplot as plt

rng = np.random.RandomState(123)

d = 2       # 데이터의 차원
N = 10      # 데이터 수
mean = 5    # 뉴런이 발화하는 데이터의 평균값

x1 = rng.randn(N, d) + np.array([0, 0])
x2 = rng.randn(N, d) + np.array([mean, mean])

plt.scatter(x1[:, [0]], x1[:, [1]], color='r', marker='o', label='x1')
plt.scatter(x2[:, [0]], x2[:, [1]], color='b', marker='x', label='x2')
plt.axis(xmin=-1, xmax=7, ymin=-1, ymax=7)
plt.grid()
plt.legend()
plt.show()

X = np.concatenate((x1, x2), axis=0)     # x1과 x2의 데이터를 합쳐서 입력 데이터로 만든다

• 퍼셉트론 모델에 필요한  매개변수 웨이트 벡터 $\mathbb{w}$와 바이어스 $b$를 초기화하고, 출력값은 $y=f(\mathbb{wx}+b)$를 코드로 정의한다

W = np.zeros(d)
b = 0

def H(X):  # 퍼셉트론 모델의 예측 출력값
    return step(np.dot(W, X) + b)

def step(X):    # 활성화 함수
    return 1 * (X > 0)

def y(i):       # i번째 학습의 결과의 실제의 값
    if i < N:
        return 0    # x1에 속하는 N-1개까지는 발화하지 않기 때문에 0
    else:
        return 1    # x2에 속하는 N개부터는 발화하기 때문에 1 

• 오차정정학습법은 모든 데이터를 정확하게 분류할 때까지 학습을 반복하기 때문에 반복문을 다음과 같이 유사코드로 작성할 수 있다

while True:
    #
    # 매개변수 업데이트 처리
    #
    
    if '모든 데이터를 정확하게 분류했다면':
        break 

• 매개변수 업데이트 부분에는 식 (3.7)~식 (3.10)을 구현해야할 뿐만 아니라 데이터 분류가 제대로 되었는지 판별할 수 있도록 구현한 코드는 다음과 같다

while True:
    classified = True:
    
    for i in range(N * 2):

        delta_W = (y(i) - H(X[i])) * X[i]     # 식 (3.7)
        delta_b = y(i) - H(X[i])              # 식 (3.8)
        
        W += delta_W                               # 식 (3.9)
        b += delta_b                               # 식 (3.10)
        
        classified *= all(delta_W == 0) * (delta_b == 0)
        
    if classified:
        break

print(f'w:\n{W}')
print(f'b:\n{b}') 

• 12라인 코드는 20개의 데이터 중에서 하나라도 $\Delta\mathbb{w}\neq 0$이거나 $\Delta b\neq 0$이면 classified 변수는 $0$, 즉 False가 되기 때문에 다시 학습을 반복하게 된다
  

 classified *= all(delta_W == 0) * (delta_b == 0)

• 최종적으로 업데이트된 매개변수의 값은 다음과 같기 떄문에 두 종류의 데이터를 구분하는 식은 $2.14037745x_1 + 1.27639271x_2 -9=0$이며 그림과 같이 구분되는 것을 알 수 있다
  

 w:
[ 2.14037745  1.2763927 ]
b:
-9

출처 : 정석으로 배우는 딥러닝

2. 논리 회로(Logic Circuit)

논리 게이트(Logic Gate)

• 디지털 회로에서는 0과 1 신호의 입출력을 제어하기 위해 논리 게이트라는 회로를 사용
• 사람의 뇌를 흉내내기 위해서 논리 게이트를 조합하여 구현할 수 있는지 여부가 가장 중요
  

• 기본적으로 3가지 논리 게이트를 사용하여 복잡한 회로를 구현

1. AND 게이트(논리곱)
2. OR 게이트(논리합)
3. NOT 게이트(논리부정)
   

AND 게이트

• AND 게이트는 그림과 같이 입력이 2개, 출력이 1개이며, 2개의 입력이 모두 $1$일 때만 $1$을 출력하고 그 외에는 $0$을 출력

Input		Output
$x_1$	$x_2$	$y$
$0$	$0$	$0$
$0$	$1$	$0$
$1$	$0$	$0$
$1$	$1$	$1$

• AND 게이트로 만든 회로는 신경망 단순 모델과 동일한 형태(입력 2개, 출력 1개)이기 때문에 신경망으로 구현 가능

• AND 게이트를 신경망으로 구현하기 위해서는 위의 표에 나온 $\mathbb{x}=(x_1,x_2)$과 $y$에 대한 각각의 값에 대하여 가설 모델(Hyperthesis model) 식 (2.1)를 만족하는 매개변수 $(w_1,w_2,\theta)$를 찾을 수 있어야 한다
  

\begin{eqnarray} H(\mathbb{x}) = \left\{ \begin{array}{ll} 1 & w_1x_1 + w_2x_2 -\theta \geqslant 0 \\ 0 & w_1x_1 + w_2x_2 -\theta< 0\end{array}\right. \tag{2.1} \end{eqnarray}

식 (2.1)가 성립하는 값 $(w_1, w_2, \theta)$를 구하는 방법의 예

• 먼저 매개변수 $(w_1,w_2,\theta)$에 임의의 값을 넣고 $(x_1,x_2)$의 모든 값에 대하여 예측 모델의 계산한 값 $H(\mathbb{x})$와 실제 값인 $y$의 차가 작아지도록 $(w_1,w_2,\theta)$ 값을 다시 조정해야한다

• 예를 들어, 매개변수를  $(w_1,w_2,\theta)=(1, 1, 0)$으로 하면 $(x_1,x_2)=(0,0)$일 때 식 (2.1)를 계산해보면 $H(\mathbb{x})=1\cdot 0 + 1\cdot 0 - 0 =0\geqslant 0$이 되어 $H(\mathbb{x})=1$이 되어 발화가 되나, 실제로는 $y=0\neq H(\mathbb{x})$이 되어 발화되어서는 안된다

• 이는 뉴런끼리의 결합이 강하거나 임계값이 낮아서 발생하는 일이기 때문에 가중치를 낮추거나 임계값을 높이는 방법으로 출력을 낮게 만들어야 함

오차정정학습법(Error Correction Learning)

• 위의 예처럼 임의의 매개변수 $(w_1,w_2,\theta)$에 대하여 식 (2.1)를 계산한 값 $H(\mathbb{x})$에 대하여 $H(\mathbb{x})\neq y$라면 매개변수$(w_1,w_2,\theta)$를 다시 수정하면서 $H(\mathbb{x})\cong y$가 되도록 하는 방법을 오차정정학습법이라고 하며 이와 같이 결과값을 보고 가중치를 수정하기 때문에 역전파 알고리즘(backward propagation algorithm)이라고 함

• 정답인 출력값을 $y$라 하고, 신경망 모델의 출력값을 $H(\mathbb{x})$라고 하면 오차정정학습법을 다음과 같이 정리할 수 있음

• $y=H(\mathbb{x})$일 경우, 정확한 값이 출력되었기에 매개변수를 수정할 필요가 없다
• $y=0$일 때 $H(\mathbb{x})=1$인 경우, 출력값이 크기 때문에 출력값을 작게하는 방향으로 매개변수를 조정한다
• 입력값이 양수이면 가중치를 작게, 임계값은 높게
  
• 입력값이 음수이면 가중치를 크게, 임계값은 높게
  
• $y=1$일 때 $H(\mathbb{x})=0$인 경우, 출력값이 작기 때문에 출력값을 크게하는 방향으로 매개변수를 조정한다
• 입력값이 양수이면 가중치를 크게, 임계값은 낮게
  
• 입력값이 음수이면 가중치를 작게, 임계값은 낮게

• 이전 매개변수 $(w_1,w_2,\theta)$와 새로 업데이트된 매개변수 $(w'_1,w'_2,\theta')$와의 차이를 각각 $\Delta w_1$과 $\Delta w_2$, $\Delta \theta$라고 하면 각각의 차이는 식 (2.2), 식 (2.3), 식 (2.4)와 같이 정의 가능
  

\begin{align} \Delta w_1 & = (y - H(\mathbb{x}))x_1\tag{2.2}\\ \Delta w_2 & = (y - H(\mathbb{x}))x_2 \tag{2.3}\\ \Delta\theta & =  -(y-H(\mathbb{x}))\tag{2.4}\end{align}

• 오차정정학습법에 따라 $y=0$일 때 $H(\mathbb{x})=1$인 경우, 출력값이 크기 때문에 출력값을 작게하는 방향으로 매개변수를 조정해야 하는데, AND 게이트에서 입력값은 모두 0보다 크거나 같은 양수이기 때문에 가중치를 작게 만들고 임계값은 높게 만들어야 한다
  
• 식 (2.2)는 $\Delta w_1=y-H(\mathbb{x}) = 0 - 1= -1$
  
• 식 (2.3)는 $\Delta w_1=y-H(\mathbb{x}) = 0 - 1= -1$
• 식 (2.4)는 $\Delta \theta = -(y-H(\mathbb{x})) = -(0-1) = 1$

• 반면에 $y=1$일 때 $H(\mathbb{x})=0$인 경우, 출력값이 작기 때문에 출력값을 크게하는 방향으로 매개변수를 조정해야 하는데, AND 게이트에서 입력값은 모두 0보다 크거나 같은 양수이기 때문에 가중치를 크게 만들고 임계값은 낮게 만들어야 한다
  
• 식 (2.2)는 $\Delta w_1=y-H(\mathbb{x}) = 1 - 0= 1$
  
• 식 (2.3)는 $\Delta w_1=y-H(\mathbb{x}) = 1 - 0= 1$
• 식 (2.4)는 $\Delta \theta = -(y-H(\mathbb{x})) = -(1-0) = -1$

•  위의 두 경우를 따져본 결과 식 (2.2)와 식 (2.3), 식 (2.4)는 올바르게 정의한 예로 볼 수 있다

• 이제 $k$번째 오차정정으로 얻은 매개변수를 $(w^k_1,w^k_2,\theta^k)$라고 하면 $k+1$번째 오차정정으로 얻은 각각의 매개변수는 식 (2.5), 식 (2.6), 식 (2.7)과 같이 정의 가능
  

\begin{align} w^{k+1}_1 & = w^k_1 + \Delta w_1^k\tag{2.5}\\ w^{k+1}_2 & = w^k_2 +\Delta w_2^k \tag{2.6}\\ \theta^{k+1} & =  \theta^k + \Delta\theta^k\tag{2.7}\end{align}

• 오차정정학습법은 $k$번째 반복 학습에서 매개변수를 업데이트하고 다시 $k+1$번째 반복 학습을 하면서 매개변수를 다시 업데이트하면서 오차가 최대한으로 작아져 정답이 출력될 때까지 알고리즘을 반복하는 방식으로 진행

• 이 과정은 아래 표와 같이 각각의 매개변수들이 업데이트되면서 학습이 반복될 수록 오차가 줄어들면서 정확한 값을 출력하는 것을 알 수 있다
  

• 오차정정학습법은 '정확한 출력이 나올 때까지 매개변수를 업데이트를 반복하는 과정'을 말하며 '신경망을 학습시킨다'라고 부르며 학습의 결과로 매개변수 $(w_1, w_2, \theta) = (2, 1, 3)$이 구해졌기 때문에 뉴런이 발화하는 경계는 식 (2.8)에 의해 결정된다는 것을 알 수 있으며, 아래 그림과 같다

• 아래 그림을 보면 식 (2.8)의 직선 이 외에도 다양한 직선으로도 데이터를 분류할 수 있음을 알 수 있는데, 이는 오류정정학습법을 통해 얻은 모델이 데이터를 잘 분류할 수 있는 모델 중의 하나인 것을 알 수 있다
  

$\begin{eqnarray} 2\cdot x_1 + 1\cdot x_2 - (3) = 2x_1 + x_2 - 3 = 0 \tag{2.8}\end{eqnarray}$

OR 게이트

• OR 게이트는 그림과 같이 입력이 2개, 출력이 1개이며, 2개의 입력 중 하나라도 $1$이면 $1$을 출력하고 그 외에는 $0$을 출력

Input		Output
$x_1$	$x_2$	$y$
$0$	$0$	$0$
$0$	$1$	$1$
$1$	$0$	$1$
$1$	$1$	$0$

• OR 게이트도 AND 게이트와 형태가 같기 때문에 신경망 단순 모델과 동일한 형태(입력 2개, 출력 1개)이기 때문에 신경망으로 구현 가능

• OR 게이트를 신경망으로 구현하기 위해서는 위의 표에 나온 $(x_1,x_2,y)$에 대한 각각의 값에 대하여 식 (2.1)를 만족하는 매개변수 $(w_1,w_2,\theta)$를 찾을 수 있어야 한다

\begin{eqnarray} H(\mathbb{x}) = \left\{ \begin{array}{ll} 1 & w_1x_1 + w_2x_2 -\theta \geqslant 0 \\ 0 & w_1x_1 + w_2x_2 -\theta< 0\end{array}\right. \tag{2.1} \end{eqnarray}

• AND 게이트와 당일한 방식으로 오차정정학습법을 사용하면 아래 표와 같은 결과를 얻을 수 있다

• 오류정정학습법을 통해 매개변수 $(w_1, w_2, \theta) = (2, 1, 3)$이 구해졌기 때문에 뉴런이 발화하는 경계는 식 (2.9)에 의해 결정된다는 것을 알 수 있으며, 이 결과는 아래 그림과 같이 표현할 수 있다
  

$\begin{eqnarray} 1\cdot x_1 + 1\cdot x_2 -( 1) = x_1 + x_2 -1 = 0 \tag{2.9}\end{eqnarray}$

NOT 게이트

• NOT 게이트는 AND 게이트나 OR 게이트와는 달리 아래 그림처럼 입력이 1개, 출력이 1개이며, 입력이 $0$이면 $1$을 출력하고, 입력이 $1$이면 $0$을 출력

Input	Output
$x_1$	$y$
$0$	$1$
$1$	$0$

• NOT 게이트도 신경망 단순 모델에서 입력 1개이고 출력이 1개인 신경망으로 구현 가능

• NOT 게이트는 입력이 1개이기 때문에 식 (2.10)과 같이 표현할 수 있다

\begin{eqnarray} H(x) = \left\{ \begin{array}{ll} 1 & wx -\theta \geqslant 0 \\ 0 & wx -\theta< 0\end{array}\right. \tag{2.10} \end{eqnarray}

• NOT 게이트는 신호를 반전시키는 것이기 때문에 $w=-1$이고 $\theta=-1$이면 식 (2.1)을 만족하는 것을 알 수 있다

\begin{eqnarray} y = \left\{ \begin{array}{ll} wx  -\theta = -1\cdot 0 - (-1)=0 + 1 = 1 & \textrm{where }\, x=0\\ wx -\theta = -1\cdot 1 - (-1) = -1 + 1 = 0 &\textrm{where }\, x=1\end{array}\right. \tag{2.11} \end{eqnarray}

NOT 게이트의 오차정정학습법

• 식 (2.11)은 직관적으로 얻은 결과이지만 AND 게이트와 OR 게이트처럼 오류정정학습법을 통해 매개변수 $(w_1,\theta)$의 값을 구해보자

• AND 게이트에서 정의했던 것과 같이 $\Delta w_1$과 $\Delta \theta$는 각각 식 (2.12)와 식 (2.13)과 같이 정의할 수 있다

\begin{align} \Delta w & = (y- H(\mathbb{x}))x \tag{2.12}\\ \Delta \theta & =  -(y - H(\mathbb{x})) \tag{2.13}\end{align}

• 또한 $k$번째 오차정정학습법을 통해 얻은 매개변수를 $(w^k_1, \theta^k_1)$라고 하면 각각의 $k+1$번째 오차정정을 통해 얻은 각각의 매개변수는 식 (2.14)와 식 (2.15)와 같이 정의할 수 있다
  

\begin{align} w^{k_1} &= w^k + \Delta w \tag{2.14}\\ \theta^{k+1} &= \theta^k + \Delta \theta  \tag{2.15}\end{align}

• 식 (2.14)와 식 (2.15)를 가지고 오차정정학습 과정을 진행하면 다음과 같은 결과를 얻을 수 있다

• 오차정정학습법을 통해 매개변수 $(w_1, \theta) = (-1, -1)$이 구해졌기 때문에 뉴런이 발화하는 경계는 식 (2.16)에 의해 결정된다는 것을 알 수 있으며, 이 결과는 아래 그림과 같이 표현할 수 있음
  

$\begin{eqnarray} -1\cdot x_1 -(-1) = -x_1 + 1 = 0 \tag{2.9}\end{eqnarray}$

출처 : 정석으로 배우는 딥러닝

Neural Network의 단순 모델

사람 뇌의 내부는 뉴런(neuron)들의 네트워크로(neural network) 이루어져 있으며, 네트워크에는 전기가 흐르고 있기 때문에 사람의 뇌는 하나의 네트워크로 구성되어 있다고 생각할 수 있음

• 뉴런은 전기신호를 통해 다른 뉴런에게 정보를 전달
• 뉴런이 어떤 임계값(threshold) 이상의 전기신호를 받으면 발화(spike)해서 다른 뉴런에게 전기신호를 전달하는데 이런 기능이 네트워크 안에서 전기의 흐름을 제어

신경망과 딥러닝

• 사람의 뇌는 뉴런이 서로 연결되어 있는 네트워크 구조로 되어있기 때문에 신경망(nueral network)이라는 명칭을 사용

• 사람의 뇌는 매우 복잡한 구조로 되어 있기 때문에 뇌를 모델링하는 하는 방법는 신경망 알고리즘을 연구하는데 매우 중요

• 신경망 알고리즘을 이해하고 구현하기 위해서는 아래 그림과 같이 전기신호가 뉴런 사이에서 전달되는 형태를 모델로 만드는 방법을 고려해야 함

출처: http://rpi-cloudreassembly.transvercity.net/wp-content/uploads/2012/11/NeuralNetwork1-copy-1024x444.jpg

• 뉴런의 네트워크 안에서 신호가 계층적으로 처리된다는 것은 오래 전에 입증되었음

• 예를 들면 아래 그림과 같이 눈의 망막을 통해 들어온 정보가 점에 응답하는 뉴런 층에 전달되고, 그 뉴런 층에서 출력된 전기신호는 선에 응답하는 뉴런 층에 전달되고, 다시 전체 윤곽에 응답하는 층으로 전달되고, 이것이 더욱 자세한 부분으에 응답하는 층으로 전달되는 방식으로 진행되어 최종적으로는 우리가 지각하는 사물의 형태로 인식함
• 딥러닝(Deep Learning)은 이런 깊은 계층 구조를 모델링한 신경망

어떤 뉴런(출력)이 2개의 뉴런(입력)으로부터 전기신호를 받는 단순 뉴럴 네트워크 모델을 생각할 때 고려해야할 사항은?

1. 2개의 뉴런 중 어느 것이 어느 정도의 전기신호를 받는가?
2. 임계값은 어느 정도로 설정해야 하는가?
3. 임계값을 넘었을 때 어느 정도의 전기신호를 보내는가?

2개 뉴런이 얼마만큼의 전기신호를 받는지를 \(x_1\)과 \(x_2\)로 표시

• 2개의 뉴런은 다음 뉴런에게 전기신호를 전달하는 역할을 하기 때문에 임계값이 없으며
• 2개의 뉴런은 결합 강도가 다르기 때문에 실제로 전달되는 전기신호의 양도 다름

2개 뉴런의 결합 강도를 \(w_1\)과 \(w_2\)로 표시

• 아래 그림과 같이 2개 뉴런으로 부터 전달되는 전기신호의 양은 식 (1)과 같으며, \(w_1\)과 \(w_2\)를 가중치(weight)라고 함

\begin{eqnarray} w_1x_1 + w_2x_2 \tag{1.1} \end{eqnarray}

전기신호를 전달받은 뉴런이 다음 뉴런으로 전기신호를 전달하는 기준은 임계값

• 전기신호를 받은 뉴런이 발화할 것인지는 전달받은 전기신호의 양이 임계값을 넘었는지 넘지 않았는지에 따라 결정되며 이 값이 편향 또는 바이어스(bias)이다
• 임계값을 \(\theta\)라고 했을 때 \(w_1x_1 + w_2x_2 \geqslant \theta\)를 만족하면 뉴런이 발화하고 \(w_1x_1 + w_2x_2 < \theta\)이면 발화하지 않음
• 뉴런이 발화할 때 다음 뉴런으로 전기량이 얼마나 전해지는지에 관한 정보는 네트워크의 가중치가 가지고 있기 때문에 뉴런의 발화에 관해서는 1(발화했다)과 0(발화하지 않았다)의 두 가지 경우만을 고려하면 됨

이전 뉴런으로부터 받는 전기신호의 양을 \(y\)라고 하면 신경망의 단순 모델은 식 (2)로 나타낼 수 있음

\begin{eqnarray} y = \left\{ \begin{array}{ll} 1 & w_1x_1 + w_2x_2 \geqslant \theta \\ 0 & w_1x_1 + w_2x_2 < \theta\end{array}\right. \tag{1.2} \end{eqnarray}

• 신경망의 가중치 \(w_1\)과 \(w_2\)와 임계값 \(\theta\)를 알맞게 설정한다면 입력 \(x_1\)과 \(x_2\)에 대한 출력 \(y\)값이 실제 사람의 뇌에서 전달되는 전기신호량과 같게 만들 수 있음
• 아무리 복잡한 신경망이라도 단순 모델을 사용하여 구현할 수 있음

출처 : 정석으로 배우는 딥러닝