비선형 분류(Non-Linear Classification)
- XOR(배타논리) 게이트는 아래 그림과 같으며 입출력은 아래 표와 같다
Input |
Output |
|
$x_1$ |
$x_2$ |
$y$ |
$0$ |
$0$ |
$0$ |
$0$ |
$1$ |
$1$ |
$1$ |
$0$ |
$1$ |
$1$ |
$1$ |
$0$ |
XOR 게이트를 좌표평면 상에 그래프로 나타내면 아래 그림처럼 AND 게이트나 OR 게이트와는 달리 직선 하나로 데이터를 분류할 수 없다
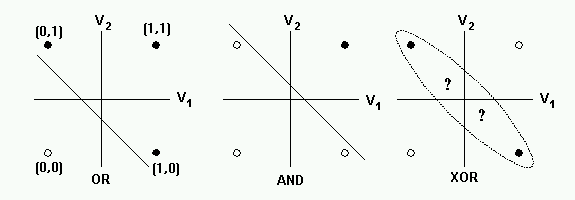
출처 : http://solarisailab.com/wp-content/uploads/2017/05/xor_limitation.gif
- XOR 게이트의 데이터를 분류하기 위해서는 적어도 2개의 데이터가 필요
출처 : http://needjarvis.tistory.com/181
- AND 게이트나 OR 게이트처럼 직선 하나($K$ 클래스인 경우에는 $K-1$개의 직선)으로 데이터를 분류하는 것을 '선형 분리 가능(linearly seperable)하다'고 하며 XOR 게이트처럼 직선 하나로 분류할 수 없는 경우를 '선형 분리 불가능(linearly non-seperable)하다'고 한다
- 단순 퍼셉트론이나 로지스틱 회귀처럼 선형 분리 가능한 문제에만 적용할 수 있는 모델을 선형 분류기(linear classifier)라고 한다
- 데이터가 $n$차원인 경우에는 $n-1$차원의 초평면으로 분리가 가능한지 알아봐야 하며, 분리가 안되는 경우에는 데이터의 차원을 강제로 높여서 더 높은 차원의 초평면으로 분리하는 방법 중의 하나가 SVM(Support Vector Machine) 알고리즘
XOR 게이트 구현을 위하여 게이트 조합하기
- AND, OR, NOT의 기본 게이트들은 선형 분리 가능하기 때문에 이들을 아래 그림과 같이 조합하여 구현하면 선형 분리 불가능한 XOR 게이트를 선형으로 분리할 수 있다
- XOR 게이트를 기본 게이트들의 조합으로 구성할 수 있다는 것은 신경망 모델에서 있어서 매우 중요
- 뉴런을 기본 게이트로 구성할 수 있기 때문에 비선형 분류를 할 수 있는 뉴런 모델을 기본 게이트의 조합으로 구현 가능
- 비선형 분류를 위해서는 여태까지 구현했던 것처럼 입력과 출력만 생각해서는 안된다
- 기존 신경 모델에 아래 그림 6.1처럼 점선 내부에 기본 게이트들을 추가한다
그림 6.1 기본 게이트를 조합해서 만든 XOR 게이트 모델
- 위 그림 6.1에서 점선 부분만 따로 뗴어내면 입력이 2개, 출력이 2개이 때문에 신경망 모델에서는 아래 그림 6.2처럼 2개의 뉴런을 추가하여 위 그림 6.1의 점선 부분처럼 입력이 2개, 출력도 2개로 나타낼 수 있다
그림 6.2 XOR 게이트를 신경망으로 구현한 모델
신경망 모델이 XOR 게이트를 제대로 구현한 것인가?
- 위에서 구현한 신경망 모델 그림 6.2가 XOR 게이트를 제대로 재현한 것인지 검증해보자
- 위 그림 6.2의 신경망 모델에서 뉴런의 구조는 우리가 앞에서 해왔던 것에서 변한 것이 없기 때문에 식 (6.1)과 식 (6.2), 식 (6.3)으로 나타낼 수 있다
\begin{align}h_1 &= f(w_{11}x_1+w_{12}x_2+b_1) \tag{6.1}\end{align}
\begin{align}h_2 &= f(w_{21}x_1+w_{22}x_2+b_2) \tag{6.2}\end{align}
\begin{align}y &=f(v_1h_1 + v_2h_2+c) \tag{6.3}\end{align}
- 그림 6.1에 맞추기 위해 우리는 활성화 함수 $f(\cdot)$로 계단 함수를 사용하겠지만 지금까지 살펴본 것처럼 함수의 내용이 양이냐 음이냐에 따라 출력값이 정해진다는 점에서 시그모이드 함수를 사용해도 문제되지 않는다
- 식 (6.1)과 식 (6.2), 식 (6.3)에 다음의 값을 대입하면 식 (6.4)와 식 (6.5), 그리고 신경망 모델의 가설식 (6.6)을 얻을 수 있다
\begin{eqnarray} W=\left( \begin{array}{cc} w_{11} & w_{12} \\ w_{21} & w_{22} \end{array}\right) = \left( \begin{array}{rr} 2 & 2 \\ -2 & -2 \end{array}\right)\end{eqnarray}
\begin{align} b= \left(\begin{array}{c}b_1 \\ b_2 \end{array}\right) = \left(\begin{array}{c} 2 \\ 2 \end{array}\right)\end{align}
\begin{align} v= \left(\begin{array}{c}v_1 \\ v_2 \end{array}\right) = \left(\begin{array}{c} 2 \\ 2 \end{array}\right)\end{align}
\begin{align} c = -3 \end{align}
\begin{align}h_1 &= f(2x_1+2x_2-1) \tag{6.1}\end{align}
\begin{align}h_2 &= f(-2x_1-2x_2+3) \tag{6.2}\end{align}
\begin{align}H(x) &=f(2h_1 +2h_2-3) \tag{6.3}\end{align}
- 식 (6.4)와 식 (6.5), 식 (6.6)을 토대로 XOR 게이트의 입력값을 계산해보면 가설식의 출력이 XOR 게이트의 출력과 같기때문에 신경망으로 XOR 게이트를 재현할 수 있다는 것을 알 수 있다
$\,\,x_1\,\,$ |
$\,\,x_2\,\,$ |
$\,\,\,\, y\,\,\,\,$ |
$\,\,w_{11}x_1+w_{12}x_2+b_1\,\,$ |
$h_1(x)$ |
$w_{21}x_1+w_{22}x_2+b_2$ |
$h_2(x)$ |
$v_1h_1+v_2h_2+c$ |
$H(x)$ |
$0$ |
$0$ |
$0$ |
$\,\,2\cdot0+2\cdot0-1=-1\,\,$ | $0$ | $-2\cdot0-2\cdot0+3=-1$ |
$0$ |
$2\cdot0+2\cdot0-3=-1$ |
$0$ |
$0$ |
$1$ |
$1$ |
$2\cdot0+2\cdot1-1=1$ |
$1$ | $-2\cdot0-2\cdot1+3=1$ | $1$ | $2\cdot1+2\cdot1-3=1$ |
$1$ |
$1$ |
$0$ |
$1$ |
$2\cdot1+2\cdot0-1=1$ |
$1$ | $-2\cdot1-2\cdot0+3=1$ | $1$ |
$2\cdot1+2\cdot1-3=1$ |
$1$ |
$1$ |
$1$ |
$0$ |
$2\cdot1+2\cdot1-1=3$ |
$1$ | $-2\cdot1-2\cdot1+3=-1$ |
$0$ | $2\cdot1+2\cdot0-3=-1$ |
$0$ |
- 다층 퍼셉트론(MLP; Multi-Layer Perceptron) : 입력과 출력 이외의 뉴런이 연결된 모델
- 다층 퍼셉트론이라는 이름에서 알 수 있듯이 신겸앙 모델은 인간의 뇌와 마찬가지로 뉴런이 층을 이루어 연결되어 있다고 생각할 수 있다
- 입력층(Input Layer) : 입력을 받는 층
- 출력층(Output Layer) : 출력하는 층
- 은닉층(Hidden Layer) : 입력층과 출력층 사이에 추가된 층
다층 퍼셉트론의 모델링
- '입력층 - 은닉층 - 출력층'이라는 3층 네트워크 구조로 만들면 XOR 게이트처럼 선형 분리 불가능한 데이터도 분리 가능하기 때문에 MLP 모델을 일반화하면 더욱 복잡한 데이터도 분류 가능
- MLP 모델의 일반화를 위해 3층 신경망을 일반화했을 때의 모델은 그림 6.3과 같이 나타낼 수 있다
그림 6.3 3층 신경망 구조
- '입력층 - 은닉층' 부분만 따로 살펴보면 지금까지 봐왔던 신경망 모델과 같은 모양이기 때문에 은닉층의 출력을 나타나는 식은 가중치 $\boldsymbol{W}$, 바이어스 $\mathbb{b}$, 활성화 함수 $f(\cdot)$일 때, 식 (6.7)과 같다
\begin{eqnarray} \mathbb{h} = f(\boldsymbol{W}\mathbb{x} + \mathbb{b})\tag{6.7}\end{eqnarray}
- 식 (6.7)로 구한 $\mathbb{h}$는 출력층에 대하여 입력층으로 전기신호를 전달하기 때문에 '은닉층 - 출력층' 부분은 가중치 $\boldsymbol{V}$, 바이어스 $\mathbb{c}$, 활성화 함수 $g(\cdot)$일 때, 식 (6.8)과 같으며, 이를 가설식으로 만들면 식 (6.9)로 표기할 수 있다
\begin{eqnarray} y = g(\boldsymbol{V}\mathbb{h} + \mathbb{c})\tag{6.8}\end{eqnarray}
\begin{eqnarray} H(\mathbb{x}) = g(\boldsymbol{V}\mathbb{h} + \mathbb{c})=g\big(\boldsymbol{V}\cdot f(\boldsymbol{W}\mathbb{x} + \mathbb{b}) +\mathbb{c}\big)\tag{6.9}\end{eqnarray}
- 활성화 함수 $g$는 신경망 모델의 전체 출력이기 때문에 다중 클래스 분류를 할 때에는 소프트맥스 함수를 사용하면 되고, 이진 분류를 하는 경우에는 시그모이드 함수를 사용하면 된다
- 활성화 함수 $f$는 출력층에 신호를 전달하는 역할을 하며, $g(\cdot)$ 안에 있는 $\boldsymbol{V}\mathbb{h}+\mathbb{c}$는 임의의 실수이기만 하면 되기 때문에 $\mathbb{h}$를 출력하는 활성화 함수 $f$는 입력값이 작으면 출력도 작은 값을 출력하고, 입력값이 크면 출력도 큰 값을 출력하는 함수이면 충분하지만 계산의 편의성을 위해 시그모이드 함수를 사용한다
다층 신경망 모델식 최적화 문제와 역전파 모델
- 다층 신경망 모델에서 학습을 시킨다하는 것은 식 (6.9) 가설식과 실제의 값 $\mathbb{y}$의 차를 최소로 만드는 매개변수 $\boldsymbol{W}$와 $\boldsymbol{V}$, $\mathbb{b}$, $\mathbb{c}$를 찾는 최적화 문제가 되는데, 신경망 모델의 핵심이 되는 오차 역전파 모델에 대해 자세히 알아보기 위해 각 층에 있는 웨이트 행력을 벡터로 분해해서 경사하강법 모델을 해석해보자
- 오차함수를 $E$라고 하면 $E=E(\boldsymbol{W}, \boldsymbol{V}, \mathbb{b}, \mathbb{c})$가 되며, 이 때 경사하강법을 통해 가장 적합한 매개변수를 찾으면 된다
- 각 매개변수에 관한 경사를 구하기 위해여, 각각의 매개변수로 편미분을 구해야하기 때문에 지금까지 한 것처럼 $N$개의 입력 데이터가 있다고 가정하고 그 중에서 $n$번째에 해당하는 데이터 벡터를 $x_n$과 $y_n$이라고 하자
- $N$개의 데이터 각각에서 발생하는 오차 $E_n$ $(n=1,2,\ldots,N)$은 서로 독립적으므로 식 (6.10)과 같이 나타낼 수 있다
\begin{eqnarray} E = \sum_{n=1}^N E_n \tag{6.10}\end{eqnarray}
- 은닉층과 출력층에서 활성화되기 이전의 값을 각각 식 (6.11)과 식 (6.12)로 표현할 수 있다
\begin{align} \mathbb{p} = \boldsymbol{W}\mathbb{x} + \mathbb{b}\tag{6.11}\end{align}
\begin{align} \mathbb{q} = \boldsymbol{V}\mathbb{h} + \mathbb{c}\tag{6.12}\end{align}
- $\boldsymbol{W}=(\mathbb{w}_1,\mathbb{w}_2,\ldots,\mathbb{w}_J)$와 $\boldsymbol{V}=(\mathbb{v}_1,\mathbb{v}_2,\ldots,\mathbb{v}_K)$에 대해 각각 식 (6.11)과 식 (6.12)에 의해서 식 (6.13)과 식 (6.14)가 성립한다
\begin{eqnarray} \left\{\begin{array}{l}\frac{\partial E_n}{\partial \mathbb{w}_j} = \frac{\partial E_n}{\partial \mathbb{p}_j} \frac{\partial \mathbb{p}_j}{\partial \mathbb{w}_j} = \frac{\partial E_n}{\partial \mathbb{p}_j}\mathbb{x}\\\frac{\partial E_n}{\partial \mathbb{b}_j} = \frac{\partial E_n}{\partial \mathbb{p}_j} \frac{\partial \mathbb{p}_j}{\partial \mathbb{b}_j} = \frac{\partial E_n}{\partial \mathbb{p}_j}\end{array}\right.\tag{6.13}\end{eqnarray}
\begin{eqnarray} \left\{\begin{array}{l}\frac{\partial E_n}{\partial \mathbb{v}_k} = \frac{\partial E_n}{\partial \mathbb{q}_k} \frac{\partial \mathbb{q}_k}{\partial \mathbb{v}_k} = \frac{\partial E_n}{\partial \mathbb{q}_k}\mathbb{h}\\\frac{\partial E_n}{\partial \mathbb{c}_k} = \frac{\partial E_n}{\partial \mathbb{q}_k} \frac{\partial \mathbb{q}_k}{\partial \mathbb{c}_k} = \frac{\partial E_n}{\partial \mathbb{q}_k}\end{array}\right.\tag{6.14}\end{eqnarray}
- 식 (6.13)과 식 (6.14)에서 $\frac{\partial E_n}{\partial \mathbb{p}_j}$와 $\frac{\partial E_n}{\partial \mathbb{q}_k}$를 구하면 매개변수 $\boldsymbol{W}$와 $\boldsymbol{V}$에 대한 경사, 즉 편미분을 구할 수 있다
- 식 (6.14)에서 $\frac{\partial E_n}{\partial \mathbb{q}_k}$를 계산해보자
- '은닉층 - 출력층' 부분에서 활성화 함수로 소프트맥스 함수를 사용하기 때문에 다중 클래스 로지스틱 회귀 모델링에서 계산했던 방법(식 (6.16)~식 (6.23))을 사용하면 식 (6.15)를 얻을 수 있다
\begin{align} \frac{\partial E_n}{\partial \mathbb{q}_k} = - (\mathbb{y}_{n_k} - H_{n_k}(\mathbb{x}_n))\quad(\because\,\, H_{n_k}(\mathbb{x}_n)=g(\mathbb{q}_k)\,\,(6.12)) \tag{6.15}\end{align}
복습 : 다중 클래스 분류 모델의 편미분 계산
- 입력 데이터 $\mathbb{x}$가 어떤 클래스$(k)$로 분류될 확률 변수를 $C$라고 하면
- 이진 분류의 경우 : $C\in \{0,1\}$
- 다중 클래스 분류의 경우 : $C = k$ $(k=1, 2, \ldots, K)$
- 다중 클래스 분류를 위해 소프트맥스 함수를 사용하기 때문에 $\mathbb{y}_k$는 식 (6.16)과 같다
\begin{align} \mathbb{y}_k &= \textrm{softmax}(\mathbb{x})_n\,\,(n=1, 2, \ldots, N)\\&=\frac{e^{\mathbb{x}_i}}{\sum_{j=1}^ne^{\mathbb{x}_j}}\tag{6.16}\end{align}
- 이제 '은닉층 - 출력층' 부분에서 입력 데이터 $\mathbb{h}_j=f(\boldsymbol{W}\mathbb{x}_n+\mathbb{b})$가 어떤 클래스($\mathbb{y}_k)$로 분류될 확률은 $g(\cdot)$이 소프트맥스 함수이기 때문에 식 (6.17)로 표현할 수 있다
\begin{align} \textrm{Pr} (C=k|\mathbb{h}_j) &= \frac{e^{\mathbb{h}_j}}{\sum_{i=1}^Je^{\mathbb{h}_j}} \tag{6.17}\end{align}
- $\mathbb{h}_j$ $(j=1, 2, \ldots, J)$가 $k$ 클래스에 속한다면 $\mathbb{y}_j$의 $k$번째 성분인 $\mathbb{y}_{j_k}$는 $1$이지만 그 외의 $\ell\neq k$번째 성분인 $\mathbb{y}_{j_\ell}$은 $0$이기 때문에 식 (6.18)과 같이 1-of-$K$ 표현으로 나타낼 수 있다
\begin{eqnarray} \mathbb{y}_{j_{\ell}} = \left\{\begin{array}{lc} 1 & (\ell = k) \\ 0 & (\ell\neq k)\end{array}\right.\tag{6.18}\end{eqnarray}
- '은닉층 - 출력층' 부분에서 다중 클래스 분류 모델의 가설식이 식 (6.9)이고, 이 때 다중 클래스 분류 문제이기 때문에 $g(\cdot)$이 소프트맥스 함수이기 때문에 $\boldsymbol{V}$와 $\mathbb{c}$의 가장 좋은 값을 찾기 위한 가능도 함수는 식 (6.19)로 표현할 수 있다
- 각각의 $\mathbb{h}_j=f(\boldsymbol{W}\mathbb{x}_n+\mathbb{b})$에 대하여 신경망 모델의 출력값이 $\mathbb{y}_{j_k}$이 될 확률 $\textrm{Pr}(C=k|\mathbb{h}_j)$이 높아야 좋은 모델이다
\begin{align} L(\boldsymbol{V}, \mathbb{c}) &= \prod_{j=1}^J\prod_{k=1}^K\textrm{Pr}(C=k|\mathbb{h}_j)^{\mathbb{y}_{j_k}}\\ &= \prod_{j=1}^J\prod_{k=1}^K\big(g_{j_k}(\mathbb{h}_j)\big)^{\mathbb{y}_{j_k}}\tag{6.19}\end{align}
- 식 (6.19)을 최대로 만드는 매개변수 $\boldsymbol{V}$와 $\mathbb{c}$를 구하기 위해 식 (6.19)에 $\log$를 취하는 변형을 하면 식 (6.20)을 얻을 수 있다
\begin{align} E(\boldsymbol{V}, \mathbb{c}) &= -\log L(\boldsymbol{V}, \mathbb{c})\\ &= -\sum_{j=1}^J \sum_{k=1}^{K}\mathbb{y}_{j_k}\log g_{j_k}(\mathbb{h}_j)\tag{6.20}\end{align}
- 우리는 식 (6.20)이 교차 엔트로피 오차 함수로 이 식의 최적화 문제를 풀어야 가설식이 맞는 매개변수를 찾을 수 있다는 것을 알고 있다. 그리고 가장 널리 알려진 경사하강법을 통해 최적화된 매개변수를 찾을 수 있다는 것도 알고 있다
복습 : 다중 클래스 회귀 모델의 경사하강법
- '은닉층 - 출력층' 부분에서 $\mathbb{q}$의 $\ell$번째 성분인 $\mathbb{q}_\ell$의 편미분을 구해보자
- $I$를 $K$차 단위행렬이라고 하면 다음과 같이 식 (6.21)을 얻을 수 있다
\begin{align} \frac{\partial E_n}{\partial \mathbb{q}_\ell} &= -\sum_{j=1}^J\sum_{k=1}^K \frac{\partial E_n}{\partial g_{j_k}(\mathbb{q}_j)}\frac{\partial g_{j_k}(\mathbb{q}_j)}{\partial \mathbb{q}_\ell}\\ &= -\sum_{j=1}^J\sum_{k=1}^K \frac{\partial}{\partial g_{j_k}(\mathbb{q}_j)} \big(\mathbb{y}_{j_k}\log g_{j_k}(\mathbb{q}_j)\big)\frac{\partial g_{j_k}(\mathbb{h}_j)}{\partial
\mathbb{q}_\ell}\quad(\because\,\, (6.20))\\ &= -\sum_{j=1}^J\sum_{k=1}^K \frac{\mathbb{y}_{j_k}}{\log g_{j_k}(\mathbb{h}_j)} \frac{\partial g_{j_k}(\mathbb{h}_j)}{\partial
\mathbb{q}_\ell}\\ &= -\sum_{j=1}^J\sum_{k=1}^K
\frac{\mathbb{y}_{j_k}}{\log g_{j_k}(\mathbb{x}_n)} g_{j_k}(\mathbb{h}_j)\big(I_{j_k} - g_{j_k}(\mathbb{h}_j)\big)\quad(\because\,\, g_{j_k}(\mathbb{h}_j)\textrm{ is softmax})\\ &= -\sum_{j=1}^J \Bigg(\sum_{k=1}^K \mathbb{y}_{j_k} I_{j_k} - \sum_{k=1}^K \mathbb{y}_{j_k}g_{j_k}(\mathbb{h}_j)\Bigg)\\ &= -\sum_{j=1}^J \big(\mathbb{y}_{j_\ell} - g_{j_\ell}(\mathbb{h}_j)\big)\quad(\because\,\,(6.18))\\ &= -\big(\mathbb{y}_\ell - g_\ell(\mathbb{h}_j)\big)\quad(\because\,\,(6.18))\tag{6.21}\end{align}
다층 신경망 모델식 최적화 문제와 역전파 모델(계속)
- '은닉층 - 출력층' 부분의 편미분 식 (6.14)는 식 (6.21)로부터 식 (6.22)로 다시 쓸 수 있는데, 이는 지금까지 우리가 봐왔던 식과 동일한 것을 알 수 있다
\begin{align} \frac{\partial E_n}{\partial \mathbb{v}_k} &= \frac{\partial E_n}{\partial \mathbb{q}_k}\mathbb{h}= -\big(\mathbb{y}_\ell - g_\ell(\mathbb{h}_j)\big)\mathbb{h}\tag{6.22} \end{align}
- 이제 우리는 식 (6.13)의 $\frac{\partial E}{\partial \mathbb{p}_j}$를 구하면 식 (6.23)가 되기 때문에 모든 경사를 구할 수가 있다
\begin{align} \frac{\partial E_n}{\partial \mathbb{p}_j} &= \sum_{k=1}^K \frac{\partial E_n}{\partial \mathbb{q}_k} \frac{\partial \mathbb{q}_k}{\partial \mathbb{p}_j} \\ &= \sum_{k=1}^K \frac{\partial E_n}{\partial \mathbb{q}_k} \frac{\partial}{\partial \mathbb{p}_j}\big(\mathbb{v}_{k_j}f(\mathbb{p}_j)+\mathbb{c}_k \big) \quad(\because\,\, \mathbb{q}=\boldsymbol{V}f(\mathbb{p})+\mathbb{c})\\ &= \sum_{k=1}^K \frac{\partial E_n}{\partial \mathbb{q}_k} \Big( f'(\mathbb{p}_j)\mathbb{v}_{kj}\Big)\tag{6.23}\end{align}
- 식 (6.13)과 식 (6.14)를 식 (6.24)와 식 (6.25)로 정의해보면 $\delta_k$는 식 (6.21)에 의해 정답과 모델 가설식 값과의 차이이기 때문에 $\delta_k$나 $\delta_j$를 오차라고도 할 수 있다
\begin{align} \delta_j &= \frac{\partial E_n}{\partial \mathbb{p}_j} \tag{6.24}\\ \delta_k &= \frac{\partial E_n}{\partial \mathbb{q}_k} \tag{6.25}\end{align}
- 식 (6.24)와 식 (6.25)는 다시 각각 식 (6.26)과 식 (6.27)로 다시 정리할 수 있다
\begin{align} \delta_j &= \frac{\partial E_n}{\partial \mathbb{p}_j}\\ &= \sum_{k=1}^K \frac{\partial E_n}{\partial \mathbb{q}_k} \Big( f'(\mathbb{p}_j)\mathbb{v}_{kj}\Big) \\ &= f'(\mathbb{p}_j) \sum_{k=1}^K \mathbb{v}_{k_j}\delta_k\tag{6.26}\\ \delta_k &= \frac{\partial E_n}{\partial \mathbb{q}_k} \\&= -\big(\mathbb{y}_\ell - g_\ell(\mathbb{h}_j)\big)\tag{6.26}\end{align}
- 식 (6.26)에서 $\sum_{k=1}^K \mathbb{v}_{k_j}\delta_k$ 부분만 따로 떼어내 살펴보면 지금까지 살펴봤던 뉴런의 출력을 나타내는 식과 모양이 같은 것을 알 수 있다. 이는 다시 말하면 신경망 모델에서 네트워크의 입력층에서 출력층으로 향하는 순방향전파(forward propagation) 출력 모델식을 고려해 해석학적으로 살펴봤지만 오차함수 최적화를 위해 매개변수를 업데이트하기 위한 경사하강법을 해석할 때에는 그림 6.4처럼 $\delta_k$가 네트워크 상에서 출력층에서 입력층으로 전파되는 모델(error backpropagation)로 생각할 수 있다
그림 6.4 오차가 출력층에서 은닉층을 통해 입력층으로 역전파되는 모델
웨이트 행렬을 벡터로 분해하지 않고 기울기 계산하기
- 교차 엔트로피 오차 함수를 웨이트로 직접 미분을 하면 다음과 같은 식을 얻을 수 있다
\begin{align} \frac{\partial E_n}{\partial \boldsymbol{W}} &= \frac{\partial E_n}{\partial \mathbb{p}}\Big(\frac{\partial \mathbb{p}}{\partial \boldsymbol{W}}\Big) \\ &= \frac{\partial E_n}{\partial \mathbb{p}}\mathbb{x}\tag{6.27}\end{align}
\begin{align} \frac{\partial E_n}{\partial \boldsymbol{V}} &= \frac{\partial E_n}{\partial \mathbb{q}}\Big(\frac{\partial \mathbb{q}}{\partial \boldsymbol{V}}\Big) \\ &= \frac{\partial E_n}{\partial \mathbb{q}}\mathbb{h}\tag{6.28}\end{align}
- 다음과 같이 정의되는 $\mathbb{e}_\mathbb{p}$와 $\mathbb{e}_\mathbb{q}$는 각각 $\delta_j$와 $\delta_k$를 성분으로 하는 벡터이다
\begin{align} \mathbb{e}_\mathbb{p} = \frac{\partial E_n}{\partial \mathbb{p}}\tag{6.29}\end{align}
\begin{align} \mathbb{e}_\mathbb{q} = \frac{\partial E_n}{\partial \mathbb{q}}\tag{6.30}\end{align}
- 따라서 다음과 같은 식을 얻을 수 있다
\begin{align} \mathbb{e}_\mathbb{p} = f'(\mathbb{p})\odot \boldsymbol{V}\mathbb{e}_\mathbb{q}\tag{6.30}\end{align}\begin{align} \mathbb{e}_\mathbb{q} = -(\mathbb{y} - g(\mathbb{h}))\tag{6.31}\end{align}
TensorFlow로 XOR 게이트 구현
import numpy as np
import tensorflow as tf
X = np.array([[0, 0],
[0, 1],
[1, 0],
[1, 1]])
Y = np.array([[0],
[1],
[1],
[0]])
x = tf.placeholder(tf.float32, shape=[None, 2])
y = tf.placeholder(tf.float32, shape=[None, 1])- 입력층 - 은닉층 설계
- tf.trunated_normal()은 절단정규분포(truncated normal distribution)를 따르는 데이터를 생성
- tf.zeros()로 매개변수를 모두 0으로 초기화하고 오차역전파법을 적용하면 오차가 제대로 반영되지 않을 경우가 있어 절단정규분포를 사용한다는데 결과가 잘 안나온다. random_normal()로 바꿔도 잘 안된다. 뭐가 문제일까?
# 입력층 - 은닉층 W = tf.Variable(tf.truncated_normal([2, 2])) b = tf.Variable(tf.zeros([2])) h = tf.nn.softmax(tf.matmul(x, W) + b)
- 은닉층 - 출력층 설계
# 은닉층 - 출력층 V = tf.Variable(tf.truncated_normal([2, 1])) c = tf.Variable(tf.zeros([1])) hypothesis = tf.nn.sigmoid(tf.matmul(h, V) + c)
- 신경망 모델 구현
cost = -tf.reduce_sum(y * tf.log(hypothesis) + (1-y) * tf.log(1-hypothesis))
train = tf.train.GradientDescentOptimizer(learning_rate=0.1).minimize(cost)
accuracy = tf.equal(tf.to_float(tf.greater(hypothesis, 0.5)), y)
init = tf.global_variables_initializer()
sess = tf.Session()
sess.run(init)
for epoch in range(4000):
sess.run(train, feed_dict={x: X, y: Y})
if epoch % 1000 == 0:
print(f'STEP = {epoch}')
classified = accuracy.eval(session=sess, feed_dict={x: X, y: Y})
prob = hypothesis.eval(session=sess, feed_dict={x: X})
print(f'classified:\n{classified}')
print()
print(f'output probability:\n{prob}')STEP = 0 STEP = 1000 STEP = 2000 STEP = 3000 classified: [[ True] [ True] [ True] [ True]] output probability: [[0.00680913] [0.99074006] [0.9909436 ] [0.00837671]]
Keras로 XOR 게이트 구현
import numpy as np
from keras.models import Sequential
from keras.layers import Dense, Activation
from keras.optimizers import SGD
X = np.array([[0, 0],
[0, 1],
[1, 0],
[1, 1]])
Y = np.array([[0],
[1],
[1],
[0]])
model = Sequential()
# 입력층 - 은닉층
model.add(Dense(input_dim=2, units=2))
model.add(Activation('sigmoid'))
# 은닉층 - 출력층
model.add(Dense(units=1))
model.add(Activation('sigmoid'))
model.compile(loss='binary_crossentropy', optimizer=SGD(lr=0.1))
model.fit(X, Y, epochs=4000, batch_size=4)
classes = model.predict_classes(X, batch_size=4)
prob = model.predict_proba(X, batch_size=4)
print(f'classified:\n{Y==classes}')
print()
print(f'output probability:\n{prob}')4/4 [==============================] - 0s 0us/step - loss: 0.1658 Epoch 3993/4000 4/4 [==============================] - 0s 251us/step - loss: 0.1656 Epoch 3994/4000 4/4 [==============================] - 0s 251us/step - loss: 0.1654 Epoch 3995/4000 4/4 [==============================] - 0s 0us/step - loss: 0.1652 Epoch 3996/4000 4/4 [==============================] - 0s 0us/step - loss: 0.1650 Epoch 3997/4000 4/4 [==============================] - 0s 250us/step - loss: 0.1648 Epoch 3998/4000 4/4 [==============================] - 0s 250us/step - loss: 0.1647 Epoch 3999/4000 4/4 [==============================] - 0s 0us/step - loss: 0.1645 Epoch 4000/4000 4/4 [==============================] - 0s 250us/step - loss: 0.1643 classified: [[ True] [ True] [ True] [ True]] output probability: [[0.17661843] [0.86831385] [0.85175645] [0.14821118]]
출처 : 정석으로 배우는 딥러닝
'신경망(Neural Network) 스터디' 카테고리의 다른 글
| 8. 경사 소실 문제 해결하기 (0) | 2018.01.18 |
|---|---|
| 7. 심층 신경망 (0) | 2018.01.10 |
| 5. 다중 클래스 로지스틱 회귀 (0) | 2017.12.27 |
| 4. 로지스틱 회귀 (0) | 2017.12.23 |
| 3. 단순 신경망 모델의 확장 (0) | 2017.12.22 |
