Neural Network의 단순 모델

사람 뇌의 내부는 뉴런(neuron)들의 네트워크로(neural network) 이루어져 있으며, 네트워크에는 전기가 흐르고 있기 때문에 사람의 뇌는 하나의 네트워크로 구성되어 있다고 생각할 수 있음

• 뉴런은 전기신호를 통해 다른 뉴런에게 정보를 전달
• 뉴런이 어떤 임계값(threshold) 이상의 전기신호를 받으면 발화(spike)해서 다른 뉴런에게 전기신호를 전달하는데 이런 기능이 네트워크 안에서 전기의 흐름을 제어

신경망과 딥러닝

• 사람의 뇌는 뉴런이 서로 연결되어 있는 네트워크 구조로 되어있기 때문에 신경망(nueral network)이라는 명칭을 사용

• 사람의 뇌는 매우 복잡한 구조로 되어 있기 때문에 뇌를 모델링하는 하는 방법는 신경망 알고리즘을 연구하는데 매우 중요

• 신경망 알고리즘을 이해하고 구현하기 위해서는 아래 그림과 같이 전기신호가 뉴런 사이에서 전달되는 형태를 모델로 만드는 방법을 고려해야 함

출처: http://rpi-cloudreassembly.transvercity.net/wp-content/uploads/2012/11/NeuralNetwork1-copy-1024x444.jpg

• 뉴런의 네트워크 안에서 신호가 계층적으로 처리된다는 것은 오래 전에 입증되었음

• 예를 들면 아래 그림과 같이 눈의 망막을 통해 들어온 정보가 점에 응답하는 뉴런 층에 전달되고, 그 뉴런 층에서 출력된 전기신호는 선에 응답하는 뉴런 층에 전달되고, 다시 전체 윤곽에 응답하는 층으로 전달되고, 이것이 더욱 자세한 부분으에 응답하는 층으로 전달되는 방식으로 진행되어 최종적으로는 우리가 지각하는 사물의 형태로 인식함
• 딥러닝(Deep Learning)은 이런 깊은 계층 구조를 모델링한 신경망

어떤 뉴런(출력)이 2개의 뉴런(입력)으로부터 전기신호를 받는 단순 뉴럴 네트워크 모델을 생각할 때 고려해야할 사항은?

1. 2개의 뉴런 중 어느 것이 어느 정도의 전기신호를 받는가?
2. 임계값은 어느 정도로 설정해야 하는가?
3. 임계값을 넘었을 때 어느 정도의 전기신호를 보내는가?

2개 뉴런이 얼마만큼의 전기신호를 받는지를 \(x_1\)과 \(x_2\)로 표시

• 2개의 뉴런은 다음 뉴런에게 전기신호를 전달하는 역할을 하기 때문에 임계값이 없으며
• 2개의 뉴런은 결합 강도가 다르기 때문에 실제로 전달되는 전기신호의 양도 다름

2개 뉴런의 결합 강도를 \(w_1\)과 \(w_2\)로 표시

• 아래 그림과 같이 2개 뉴런으로 부터 전달되는 전기신호의 양은 식 (1)과 같으며, \(w_1\)과 \(w_2\)를 가중치(weight)라고 함

\begin{eqnarray} w_1x_1 + w_2x_2 \tag{1.1} \end{eqnarray}

전기신호를 전달받은 뉴런이 다음 뉴런으로 전기신호를 전달하는 기준은 임계값

• 전기신호를 받은 뉴런이 발화할 것인지는 전달받은 전기신호의 양이 임계값을 넘었는지 넘지 않았는지에 따라 결정되며 이 값이 편향 또는 바이어스(bias)이다
• 임계값을 \(\theta\)라고 했을 때 \(w_1x_1 + w_2x_2 \geqslant \theta\)를 만족하면 뉴런이 발화하고 \(w_1x_1 + w_2x_2 < \theta\)이면 발화하지 않음
• 뉴런이 발화할 때 다음 뉴런으로 전기량이 얼마나 전해지는지에 관한 정보는 네트워크의 가중치가 가지고 있기 때문에 뉴런의 발화에 관해서는 1(발화했다)과 0(발화하지 않았다)의 두 가지 경우만을 고려하면 됨

이전 뉴런으로부터 받는 전기신호의 양을 \(y\)라고 하면 신경망의 단순 모델은 식 (2)로 나타낼 수 있음

\begin{eqnarray} y = \left\{ \begin{array}{ll} 1 & w_1x_1 + w_2x_2 \geqslant \theta \\ 0 & w_1x_1 + w_2x_2 < \theta\end{array}\right. \tag{1.2} \end{eqnarray}

• 신경망의 가중치 \(w_1\)과 \(w_2\)와 임계값 \(\theta\)를 알맞게 설정한다면 입력 \(x_1\)과 \(x_2\)에 대한 출력 \(y\)값이 실제 사람의 뇌에서 전달되는 전기신호량과 같게 만들 수 있음
• 아무리 복잡한 신경망이라도 단순 모델을 사용하여 구현할 수 있음

출처 : 정석으로 배우는 딥러닝

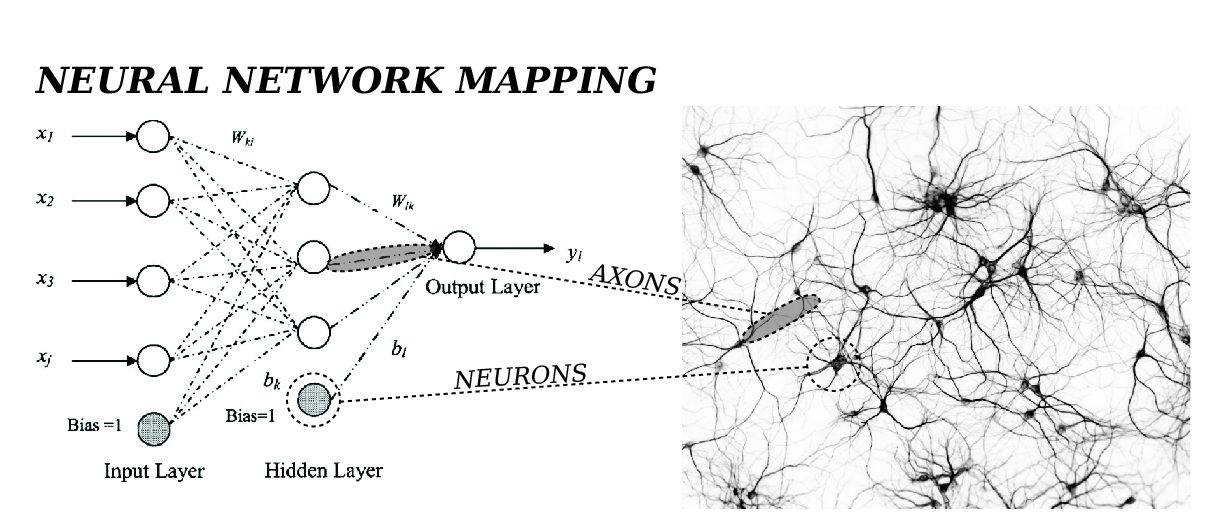
다변수 분류(Multinomial classification) : Softmax classification 연습

Softmax 함수

• \(n\)개의 값을 예측할 때 Softmax 분류 함수를 사용하여 확률분포로 만들어 준다.
  

• 아래 그림 같이 학습할 데이터 \(\mathbf{X}\)에 학습할 weight \(\mathbf{W}\)를 곱해서 예측값 \(\mathbf{Y}\)를 만드는 것으로 부터 시작한다.

• 즉, 다변수 분류에서 기본 가설식(logit) \(\mathbf{Y}\)는 식 (1)과 같다.
  

\begin{eqnarray} \mathbf{Y} = \mathbf{X} \mathbf{W} + \mathbf{b} \tag{1} \end{eqnarray}

• 그러나 식 (1)의 결과는 그냥 점수(score)에 불과하다.

• 식 (1)의 결과를 Softmax 함수에 통과시키면 결과가 확률로 나타나 분류대상에 대하여 확률분포를 만들 수 있다. 기본 가설식에 Softmax 함수를 적용한 결과가 우리가 원하는 가설식이다. 즉, 식 (2)가 가설식이다.

\begin{eqnarray} H(x) &=& \textrm{Softmax}(\mathbf{Y})\\ &=& \textrm{Softmax}(\mathbf{X} \mathbf{W} + \mathbf{b}) \tag{2} \end{eqnarray}

Softmax 함수를 사용하는 모델

• 아래 그림과 같이 TensorFlow를 사용하여 수식을 그대로 써주면 된다.

• 기본 가설식 식 (1)은 다음과 같은 코드를 사용한다.

tf.matmul(X,W) + b 

• 최종 가설식 식 (2) $H(x)$는 다음과 같은 코드를 사용하여 확률분포를 계산할 수 있다.
  

hypothesis = tf.nn.softmax(tf.matmul(X,W) + b)

• Cost(Loss) 함수 식 (3)처럼 CROSS-ENTROPY로 표현할 수 있으며, 다음과 같은 코드를 사용한다.
  

\begin{eqnarray} \textrm{Cost(Loss) ft.} = \frac{1}{N}\sum_i\mathcal{D}(S(\mathbf{W}x_i+\mathbf{b}, L_i) \tag{3}\end{eqnarray}

cost = tf.reduce_mean(-tf.reduce_sum(Y * tf.log(hypothesis), axis=1))

• 경사하강법은 다음과 같은 코드를 사용한다.
  

optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.1).minimize(cost)

Softmax 분류 함수를 사용하는 기계 학습 연습

• 학습에 사용할 데이터는 다음과 같다.

x_data = [[1, 2, 1, 1], [2, 1, 3, 2], [3, 1, 3, 4], [4, 1, 5, 5], [1, 7, 5, 5], [1, 2, 5, 6], [1, 6, 6, 6], [1, 7, 7, 7]]
y_data = [[0, 0, 1], [0, 0, 1], [0, 0, 1], [0, 1, 0], [0, 1, 0], [0, 1, 0], [1, 0, 0], [1, 0, 0]]

X = tf.placeholder("float", [None, 4])
Y = tf.placeholder("float", [None, 3])
nb_classes = 3

• 전체 코드는 다음과 같다.
  

import tensorflow as tf

x_data = [[1, 2, 1, 1], [2, 1, 3, 2], [3, 1, 3, 4], [4, 1, 5, 5], [1, 7, 5, 5],
          [1, 2, 5, 6], [1, 6, 6, 6], [1, 7, 7, 7]]

# y값은 ONE-HOT encoding을 사용해 표현
y_data = [[0, 0, 1], [0, 0, 1], [0, 0, 1], [0, 1, 0], [0, 1, 0], [0, 1, 0],
          [1, 0, 0], [1, 0, 0]]


X = tf.placeholder('float', [None, 4])
Y = tf.placeholder('float', [None, 3])
# Y값의 개수가 분류대상(label)의 개수이며, 이를 nb_classes로 설
nb_classes = 3

W = tf.Variable(tf.random_normal([4, nb_classes]), name='weight')
b = tf.Variable(tf.random_normal([nb_classes]), name='bias')

# 가설식은 softmax 함수를 사용하여 표현
hypothesis = tf.nn.softmax(tf.matmul(X, W) + b)

# Cost(Loss) 함수는 cross-entropy를 사용하여 표
cost = tf.reduce_mean(-tf.reduce_sum(Y * tf.log(hypothesis), axis=1))
optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.1).minimize(cost)

# 그래프를 만들자
with tf.Session() as sess:
    # 변수 초기화
    sess.run(tf.global_variables_initializer())

    for step in range(2001):
        # 경사하강법을 사용하여 학습을 시킨다
        sess.run(optimizer, feed_dict={X: x_data, Y: y_data})
        if step % 200 == 0:
            print(f'STEP = {step:04}, cost 함수값 = '
                  f'{sess.run(cost, feed_dict={X: x_data, Y: y_data})}')

• 결과값
  

STEP = 0000, cost 함수값 = 1.9889715909957886
STEP = 0200, cost 함수값 = 0.5703549385070801
STEP = 0400, cost 함수값 = 0.45723509788513184
STEP = 0600, cost 함수값 = 0.3804630637168884
STEP = 0800, cost 함수값 = 0.3090059161186218
STEP = 1000, cost 함수값 = 0.24136722087860107
STEP = 1200, cost 함수값 = 0.2168642282485962
STEP = 1400, cost 함수값 = 0.19778816401958466
STEP = 1600, cost 함수값 = 0.18168748915195465
STEP = 1800, cost 함수값 = 0.16792559623718262
STEP = 2000, cost 함수값 = 0.15603584051132202

ONE-HOT Encoding 테스트

• 데이터를 가지고 값을 예측해보자.

• 전체 코드의 뒤에 아래 코드를 추가한다.
  

    # ONE-HOT 인코딩 테스트
    a = sess.run(hypothesis, feed_dict={X: [[1, 11, 7, 9]]})
    print(f'예측 결과 = {a}, ONE-HOT 인코딩 결과 = {sess.run(tf.arg_max(a, 1))}')

    b = sess.run(hypothesis, feed_dict={X: [[1, 3, 4, 3]]})
    print(f'예측 결과 = {b}, ONE-HOT 인코딩 결과 = {sess.run(tf.arg_max(b, 1))}')

    c = sess.run(hypothesis, feed_dict={X: [[1, 1, 0, 1]]})
    print(f'예측 결과 = {c}, ONE-HOT 인코딩 결과 = {sess.run(tf.arg_max(c, 1))}')

    # 한번에 여러 개의 값을 넣어 테스트
    all = sess.run(hypothesis, feed_dict={X: [[1, 11, 7, 9], [1, 3, 4, 3],
                                              [1, 1, 0, 1]]})
    print(f'예측 결과 = {all}, ONE-HOT 인코딩 결과 = {sess.run(tf.arg_max(all, 1))}')

• ONE-HOT 인코딩의 결과가 제대로 나오는 것을 확인할 수 있다.
  

STEP = 0000, cost 함수값 = 8.209596633911133
STEP = 0200, cost 함수값 = 0.655610203742981
STEP = 0400, cost 함수값 = 0.5474461317062378
STEP = 0600, cost 함수값 = 0.45507490634918213
STEP = 0800, cost 함수값 = 0.3648858666419983
STEP = 1000, cost 함수값 = 0.27533501386642456
STEP = 1200, cost 함수값 = 0.22607706487178802
STEP = 1400, cost 함수값 = 0.20554673671722412
STEP = 1600, cost 함수값 = 0.1882915496826172
STEP = 1800, cost 함수값 = 0.17360061407089233
STEP = 2000, cost 함수값 = 0.16095450520515442
예측 결과 = [[  2.96840118e-03   9.97021735e-01   9.90122044e-06]], ONE-HOT 인코딩 결과 = [1]
예측 결과 = [[ 0.90273005  0.08834519  0.00892478]], ONE-HOT 인코딩 결과 = [0]
예측 결과 = [[  2.43163711e-08   3.81419144e-04   9.99618530e-01]], ONE-HOT 인코딩 결과 = [2]
예측 결과 = [[  2.96840118e-03   9.97021735e-01   9.90122044e-06]
 [  9.02730048e-01   8.83451924e-02   8.92478414e-03]
 [  2.43163711e-08   3.81419144e-04   9.99618530e-01]], ONE-HOT 인코딩 결과 = [1 0 2]

Fancy Softmax Classifier

• Cross-Entropy와 One-hot encdoing, reshape을 이용하여 조금 더 멋진 코드를 만드는 연습을 해보자.

logits을 사용하는 Softmax Cross-Entropy 함수

• logits : 기본 가설식 식 (1)의 결과값이다.

\begin{eqnarray} \textrm{logits} =  \mathbf{X} \mathbf{W} + \mathbf{b} \end{eqnarray}

• logits을 사용하여 hypothesis와 Cost(Loss) 함수를 아래 그림의 ①과 같이 작성할 수 있었다.

• Cost(Loss) 함수에서 Y의 값은 one-hot 인코딩 값이다.

• ①번 코드는 계산식에 빼기 연산 및 합과 평균 등의 계산으로 다소 복잡하다.
  

• ①번 식이 다소 복잡하기 때문에 간단히 하기위해 TensorFlow에서 softmax_cross_entropy_with_logits() 함수를 제공한다.

• 입력값 2개

• logits

• one-hot 인코딩된 Y값

• softmax_cross_entropy_with_logits() 함수값에 대하여 평균을 구하면 위 그림의 ②번 식과 같이 Cost(Loss) 값을 구할 수 있다.

softmax_cross_entropy_with_logits 함수를 사용하는 모델

• 아래 그림과 같이 동물에 대한 특징이 주어졌을 때 동물을 분류해보자.

• \(Y\) 데이터의 값을 살펴보자.

• 학습 데이터가 \(n\)개이고, \(Y\) 데이터는 1개이 때문에  \(Y\)  데이터의 차원은 [None, 1]이다.

• Y \(Y\) 의 값은 0~6 사이의 값으로 one-hot encoding 값이 아니기 때문에 변환이 필요하다.

• TensorFlow의 one_hot() 함수를 사용하면 one-hot encoding의 값으로 바꿀 수 있다.

• one-hot() 함수의 입력값은  \(Y\) 값과  \(Y\) 값의 갯수(class)가 된다. 즉, \(0\leqslant Y \leqslant 6\)이기 때문에 \(\texttt{nb_classes} = 7\)이다.

• one-hot() 함수 입력값의 rank가 \(N\)이면 출력값은 \(N+1\)이 된다.

• 예를 들어, 입력값이 [[0], [3]]이라고 하면 rank=2이다. 즉, shape=(2,1)이다.
  

• 이 때의 출력값은 [[[1000000]], [[0001000]]]이 되어 rank=3이 된다. 즉, shape(2, 1, 7)이 된다.
  

• 이러한 결과는 우리가 원하는 것이 아니다. 우리는 shape=(2, 7)을 원한다.

• TensorFlow의 reshape() 함수를 사용하면 우리가 원하는 결과를 얻을 수 있다.

• 예를 들어, 입력값이 [[0], [3]]이라고 하면 출력값은 [[1000000], [0001000]]이 되어 우리가 원하는 결과를 얻을 수 있다.

• shape에서 -1은 나머지 모든 것을 의미한다.
  

softmax_cross_entropy_with_logits 함수를 사용하는 모델의 기계 학습 연습

• 전체 소스코드는 다음과 같다.

import tensorflow as tf
import numpy as np


# 동물 학습 데이터를 불러온다.
xy = np.loadtxt('data-04-zoo.csv', delimiter=',', dtype=np.float32)
x_data = xy[:, 0:-1]
y_data = xy[:, [-1]]

print(x_data.shape, y_data.shape)

# 0<= Y <= 6
nb_classes = 7

# x1, x2, x3, ..., x16
X = tf.placeholder(tf.float32, [None, 16])
Y = tf.placeholder(tf.int32, [None, 1])

Y_one_hot = tf.one_hot(Y, nb_classes)
print("one_hot", Y_one_hot)
Y_one_hot = tf.reshape(Y_one_hot, [-1, nb_classes])
print("reshape", Y_one_hot)

W = tf.Variable(tf.random_normal([16, nb_classes]), name='weight')
b = tf.Variable(tf.random_normal([nb_classes]), name='bias')

logits = tf.matmul(X, W) + b
hypothesis = tf.nn.softmax(logits)


cost_i = tf.nn.softmax_cross_entropy_with_logits(logits=logits,
                                                 labels=Y_one_hot)
cost = tf.reduce_mean(cost_i)
optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.1).minimize(cost)

# 정확도를 파악한다
# 가설식의 값을 확률분포로 변환
prediction = tf.argmax(hypothesis, 1)
# 원래의 값과 같은지 확인
correct_prediction = tf.equal(prediction, tf.argmax(Y_one_hot, 1))
# 평균을 구해 정확도를 산출한다.
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))

with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())

    for step in range(2000):
        sess.run(optimizer, feed_dict={X: x_data, Y: y_data})

        if step % 100 == 0:
            loss, acc = sess.run([cost, accuracy], feed_dict={X: x_data,
                                                              Y: y_data})
            print(f'STEP = {step:05}, Loss = {loss:.3f}, 정확도 = {acc:.2%}')

    # 예측할 수 있는지 살펴보자
    pred = sess.run(prediction, feed_dict={X: x_data})

    for p, y in zip(pred, y_data.flatten()):
        print(f'예측여부 : [{p == int(y)}], 예측값={p:2}, 실제 Y값={int(y):2}')

• 결과값

(101, 16) (101, 1)
one_hot Tensor("one_hot:0", shape=(?, 1, 7), dtype=float32)
reshape Tensor("Reshape:0", shape=(?, 7), dtype=float32)
STEP = 00000, Loss = 7.292, 정확도 = 0.99%
STEP = 00100, Loss = 0.954, 정확도 = 70.30%
STEP = 00200, Loss = 0.566, 정확도 = 84.16%
STEP = 00300, Loss = 0.420, 정확도 = 89.11%
STEP = 00400, Loss = 0.335, 정확도 = 90.10%
STEP = 00500, Loss = 0.279, 정확도 = 94.06%
STEP = 00600, Loss = 0.238, 정확도 = 95.05%
STEP = 00700, Loss = 0.207, 정확도 = 97.03%
STEP = 00800, Loss = 0.182, 정확도 = 97.03%
STEP = 00900, Loss = 0.162, 정확도 = 97.03%
STEP = 01000, Loss = 0.146, 정확도 = 97.03%
STEP = 01100, Loss = 0.132, 정확도 = 97.03%
STEP = 01200, Loss = 0.120, 정확도 = 97.03%
STEP = 01300, Loss = 0.110, 정확도 = 99.01%
STEP = 01400, Loss = 0.101, 정확도 = 99.01%
STEP = 01500, Loss = 0.094, 정확도 = 99.01%
STEP = 01600, Loss = 0.087, 정확도 = 99.01%
STEP = 01700, Loss = 0.082, 정확도 = 99.01%
STEP = 01800, Loss = 0.076, 정확도 = 99.01%
STEP = 01900, Loss = 0.072, 정확도 = 100.00%
예측여부 : [True], 예측값= 0, 실제 Y값= 0
예측여부 : [True], 예측값= 0, 실제 Y값= 0
예측여부 : [True], 예측값= 3, 실제 Y값= 3
예측여부 : [True], 예측값= 0, 실제 Y값= 0
예측여부 : [True], 예측값= 0, 실제 Y값= 0
예측여부 : [True], 예측값= 0, 실제 Y값= 0
예측여부 : [True], 예측값= 0, 실제 Y값= 0
예측여부 : [True], 예측값= 3, 실제 Y값= 3
예측여부 : [True], 예측값= 3, 실제 Y값= 3
예측여부 : [True], 예측값= 0, 실제 Y값= 0
예측여부 : [True], 예측값= 0, 실제 Y값= 0
예측여부 : [True], 예측값= 1, 실제 Y값= 1
예측여부 : [True], 예측값= 3, 실제 Y값= 3
예측여부 : [True], 예측값= 6, 실제 Y값= 6
예측여부 : [True], 예측값= 6, 실제 Y값= 6
예측여부 : [True], 예측값= 6, 실제 Y값= 6
예측여부 : [True], 예측값= 1, 실제 Y값= 1
예측여부 : [True], 예측값= 0, 실제 Y값= 0
예측여부 : [True], 예측값= 3, 실제 Y값= 3
예측여부 : [True], 예측값= 0, 실제 Y값= 0
예측여부 : [True], 예측값= 1, 실제 Y값= 1
예측여부 : [True], 예측값= 1, 실제 Y값= 1
예측여부 : [True], 예측값= 0, 실제 Y값= 0
예측여부 : [True], 예측값= 1, 실제 Y값= 1
예측여부 : [True], 예측값= 5, 실제 Y값= 5
예측여부 : [True], 예측값= 4, 실제 Y값= 4
예측여부 : [True], 예측값= 4, 실제 Y값= 4
예측여부 : [True], 예측값= 0, 실제 Y값= 0
예측여부 : [True], 예측값= 0, 실제 Y값= 0
예측여부 : [True], 예측값= 0, 실제 Y값= 0
예측여부 : [True], 예측값= 5, 실제 Y값= 5
예측여부 : [True], 예측값= 0, 실제 Y값= 0
예측여부 : [True], 예측값= 0, 실제 Y값= 0
예측여부 : [True], 예측값= 1, 실제 Y값= 1
예측여부 : [True], 예측값= 3, 실제 Y값= 3
예측여부 : [True], 예측값= 0, 실제 Y값= 0
예측여부 : [True], 예측값= 0, 실제 Y값= 0
예측여부 : [True], 예측값= 1, 실제 Y값= 1
예측여부 : [True], 예측값= 3, 실제 Y값= 3
예측여부 : [True], 예측값= 5, 실제 Y값= 5
예측여부 : [True], 예측값= 5, 실제 Y값= 5
예측여부 : [True], 예측값= 1, 실제 Y값= 1
예측여부 : [True], 예측값= 5, 실제 Y값= 5
예측여부 : [True], 예측값= 1, 실제 Y값= 1
예측여부 : [True], 예측값= 0, 실제 Y값= 0
예측여부 : [True], 예측값= 0, 실제 Y값= 0
예측여부 : [True], 예측값= 6, 실제 Y값= 6
예측여부 : [True], 예측값= 0, 실제 Y값= 0
예측여부 : [True], 예측값= 0, 실제 Y값= 0
예측여부 : [True], 예측값= 0, 실제 Y값= 0
예측여부 : [True], 예측값= 0, 실제 Y값= 0
예측여부 : [True], 예측값= 5, 실제 Y값= 5
예측여부 : [True], 예측값= 4, 실제 Y값= 4
예측여부 : [True], 예측값= 6, 실제 Y값= 6
예측여부 : [True], 예측값= 0, 실제 Y값= 0
예측여부 : [True], 예측값= 0, 실제 Y값= 0
예측여부 : [True], 예측값= 1, 실제 Y값= 1
예측여부 : [True], 예측값= 1, 실제 Y값= 1
예측여부 : [True], 예측값= 1, 실제 Y값= 1
예측여부 : [True], 예측값= 1, 실제 Y값= 1
예측여부 : [True], 예측값= 3, 실제 Y값= 3
예측여부 : [True], 예측값= 3, 실제 Y값= 3
예측여부 : [True], 예측값= 2, 실제 Y값= 2
예측여부 : [True], 예측값= 0, 실제 Y값= 0
예측여부 : [True], 예측값= 0, 실제 Y값= 0
예측여부 : [True], 예측값= 0, 실제 Y값= 0
예측여부 : [True], 예측값= 0, 실제 Y값= 0
예측여부 : [True], 예측값= 0, 실제 Y값= 0
예측여부 : [True], 예측값= 0, 실제 Y값= 0
예측여부 : [True], 예측값= 0, 실제 Y값= 0
예측여부 : [True], 예측값= 0, 실제 Y값= 0
예측여부 : [True], 예측값= 1, 실제 Y값= 1
예측여부 : [True], 예측값= 6, 실제 Y값= 6
예측여부 : [True], 예측값= 3, 실제 Y값= 3
예측여부 : [True], 예측값= 0, 실제 Y값= 0
예측여부 : [True], 예측값= 0, 실제 Y값= 0
예측여부 : [True], 예측값= 2, 실제 Y값= 2
예측여부 : [True], 예측값= 6, 실제 Y값= 6
예측여부 : [True], 예측값= 1, 실제 Y값= 1
예측여부 : [True], 예측값= 1, 실제 Y값= 1
예측여부 : [True], 예측값= 2, 실제 Y값= 2
예측여부 : [True], 예측값= 6, 실제 Y값= 6
예측여부 : [True], 예측값= 3, 실제 Y값= 3
예측여부 : [True], 예측값= 1, 실제 Y값= 1
예측여부 : [True], 예측값= 0, 실제 Y값= 0
예측여부 : [True], 예측값= 6, 실제 Y값= 6
예측여부 : [True], 예측값= 3, 실제 Y값= 3
예측여부 : [True], 예측값= 1, 실제 Y값= 1
예측여부 : [True], 예측값= 5, 실제 Y값= 5
예측여부 : [True], 예측값= 4, 실제 Y값= 4
예측여부 : [True], 예측값= 2, 실제 Y값= 2
예측여부 : [True], 예측값= 2, 실제 Y값= 2
예측여부 : [True], 예측값= 3, 실제 Y값= 3
예측여부 : [True], 예측값= 0, 실제 Y값= 0
예측여부 : [True], 예측값= 0, 실제 Y값= 0
예측여부 : [True], 예측값= 1, 실제 Y값= 1
예측여부 : [True], 예측값= 0, 실제 Y값= 0
예측여부 : [True], 예측값= 5, 실제 Y값= 5
예측여부 : [True], 예측값= 0, 실제 Y값= 0
예측여부 : [True], 예측값= 6, 실제 Y값= 6
예측여부 : [True], 예측값= 1, 실제 Y값= 1

다변수 분류(Multinomial classification)

로지스틱 회귀 복습

• 입력값 \(x\)에 대하여 계산하는 유닛 \(W\)가 weight를 가지고 계산해 \(z\)를 출력한다.

• 결과 \(z\)를 sigmoid 함수를 통과시켜 0과 1사이의 값 \(\bar{y}\)으로 변환한다.

• \(y\) : 실제 데이터 값

• \(\bar{y}\) : 학습을 통한 예측 값

로지스틱 회귀 분류가 하는 역할

• 아래 그림과 같이 \(x_1\)과 \(x_2\)에 대하여 네모와 가위표를 분류한다는 것은 네모와 가위표를 분류하는 선을 찾아낸다는 것을 의미한다.

다변수 분류

• 다변수라는 것은 3개 이상으로 분류할 수 있는 데이터가 있다는 것이다.
  

• 예를 들어, 아래 그림과 같이 공부한 시간(\(x_1\))과 수업에 참석한 횟수(\(x_2\))에 따라 3종류의 학점(\(y\))를 준다고 가정하고 그래프로 표시하면 오른쪽 그림과 같이 될 것이다.

• 이진 분류(binary classification)만 가지고도 다변수 데이터를 분류할 수 있다.

1. \(A\)이거나 \(A\)가 아니거나

2. \(B\)이거나 \(B\)가 아니거나

3. \(C\)이거나 \(C\)가 아니거나

• 이진 분류만 가지고도 다변수 데이터를 분류가 가능

• 각각의 분류기(classifier) \(A\)와 \(B\), \(C\)를 실제로 구현할 때에는 다음과 같이 행렬로 구현을 한다.

• 위의 3개의 분류기, 즉 3개의 독립된 벡터를 가지고 계산을 해야하는데, 이렇게 하면 계산과 구현이 복잡하다.

• 그래서 weight 벡터를 하나로 합쳐서 계산하는 방법을 생각해볼 수 있다.
  

• 다음과 같이 계산한 결과 \(\bar{y}_A=H_A(x)\)와 \(\bar{y}_B=H_B(x)\), \(\bar{y}_C=H_C(x)\)는 우리가 예측한 결과가 된다.

• 3개의 독립된 벡터를 한번의 계산으로 각각의 값을 구할 수 있다.

• 3개의 가설값 \(H_A(x)\)와 \(H_B(x)\), \(H_C(x)\)은 우리가 원하는 결과가 아니다.
  

• 우리는 예측값이 0과 1 사이의 값을 가지며 예측값이 합이 1이 되는 확률분포가 되기를 원한다. 이런 결과를 나오게 하는 함수가 softmax 함수이다.
  

SOFTMAX 함수

• \(n\)개의 값을 softmax 함수에 넣으면 우리가 원하는 2개의 조건을 만족하는 값을 만들어줘 확률로 볼 수 있게 해준다.
  

1. 각각의 값 \(y_i\)는 \(0\leqslant y_i \leqslant 1\)을 만족한다.

2. \(\sum_i y_i =1\)

• 다음과 같이 예측값이 나올 확률을 구할 수가 있다.

• \(Pr(A) = 0.7\)

• \(Pr(B) = 0.2\)

• \(Pr(C) = 0.1\)

• 그러나 실제로 우리는 위의 예처럼 3개의 값이 아니라 1개의 값을 예측하도록 해야 한다. 즉, 가장 높은 확률을 갖는 값 1개를 예측값으로 만들어야 하는데 이를 'ONE-HOT' 인코딩이라고 한다.

• TensorFlow에서는 one-hot 인코딩을 위해 argmax() 함수를 지원한다.

• 이제 예측하는 모델 Hypothesis는 완성이 되었다.
  

다변수 분류에서의 Cost 함수

• 예측한 값과 실제의 값이 얼마나 차이가 나는지를 알 수 있는 cost 함수를 설계해야 한다.

• cost 함수를 최소화하도록 해서 학습 알고리즘을 완성시킬 수 있다.

• 다변수 분류에서는 Cost 함수로 CROSS-ENTROPY를 사용한다.

• 아래 그림에서 \(L\)는 실제의 값인 \(y\)이고, \(S(y)\)는 우리가 예측한 값 \(\bar{y}\)이다.

• 이 때 \(y\)와 \(\bar{y}\)의 차이(거리)는 \(\mathcal{D}(\bar{y},y)\)는 다음 식(1)과 같은 CROSS-ENTROPY로 표현할 수 있다.

\begin{eqnarray} \mathcal{D}(\bar{y},y)=-\sum_i y_i \log \bar{y}_i \tag{1}\end{eqnarray}

• CROSS-ENTROPY를 풀어쓰면 식 (2)와 같이 된다. 여기서 \(\odot\)는 벡터 원소별 곱셈(element-wise product)을 의미한다.
  

\begin{eqnarray} \mathcal{D}(\bar{y},y) &=& -\sum_i y_i \log \bar{y}_i \\ &=& \sum_i y_i \odot -\log \bar{y}_i \tag{2}\end{eqnarray}

• 식 (2)에서 \(-\log \bar{y}_i\)는 아래 그림과 같이 \(0\leqslant \bar{y}_i \leqslant 1\)일 때,  \(0\leqslant -\log \bar{y}_i < \infty\) 의 값을 가진다.

• 각각의 경우에 대하여 CROSS-ENTROPY를 계산해보자.
  

• 실제의 값이 \(y=A\)일 때
  

• \(\bar{y}=A\)인 경우에는 \(\mathcal{D}(\bar{y},y)\)이 작아져야 한다.
  

\begin{eqnarray} - \sum \left[ \begin{array}{c} 1 \\ 0 \end{array} \right] \odot \log \left[ \begin{array}{c} 1 \\ 0 \end{array} \right]  &=& \sum \left[ \begin{array}{c} 1 \\ 0 \end{array} \right] \odot -\log \left[ \begin{array}{c} 1 \\ 0 \end{array} \right]  \\ &=& \sum\left[ \begin{array}{c} 1 \\ 0 \end{array} \right] \odot  \left[ \begin{array}{c} -\log 1 \\ -\log 0 \end{array} \right] \\ &=&\sum \left[ \begin{array}{c} 1 \\ 0 \end{array} \right] \odot \left[ \begin{array}{c} 0 \\ \infty \end{array} \right] \\ &=& \sum \left[ \begin{array}{c} 0 \\ 0 \end{array} \right] \\ &=& 0+ 0 \\ &=& 0 \end{eqnarray}

• \(\bar{y} = B \neq A\)인 경우에는 \(\mathcal{D}(\bar{y},y)\)이 커져야 한다.

\begin{eqnarray} - \sum \left[ \begin{array}{c} 1 \\ 0 \end{array} \right] \odot \log \left[ \begin{array}{c} 0 \\ 1 \end{array} \right]  &=& \sum \left[ \begin{array}{c} 1 \\ 0 \end{array} \right] \odot -\log \left[ \begin{array}{c} 0 \\ 1 \end{array} \right]  \\ &=& \sum\left[ \begin{array}{c} 1 \\ 0 \end{array} \right] \odot  \left[ \begin{array}{c} -\log 0 \\ -\log 1 \end{array} \right] \\ &=&\sum \left[ \begin{array}{c} 1 \\ 0 \end{array} \right] \odot \left[ \begin{array}{c} \infty \\ 0 \end{array} \right] \\ &=& \sum \left[ \begin{array}{c} \infty \\ 0  \end{array} \right] \\ &=& \infty + 0 \\ &=& \infty \end{eqnarray}

• 실제의 값이 \(y=B\)일 때
  

• \(\bar{y}=B\)인 경우에는 \(\mathcal{D}(\bar{y},y)\)이 작아져야 한다.
  

\begin{eqnarray} - \sum \left[ \begin{array}{c} 0 \\ 1 \end{array} \right] \odot \log \left[ \begin{array}{c} 0 \\ 1 \end{array} \right]  &=& \sum \left[ \begin{array}{c} 0 \\ 1 \end{array} \right] \odot -\log \left[ \begin{array}{c} 0 \\ 1 \end{array} \right]  \\ &=& \sum\left[ \begin{array}{c} 0 \\ 1 \end{array} \right] \odot  \left[ \begin{array}{c} -\log 0 \\ -\log 1 \end{array} \right] \\ &=&\sum \left[ \begin{array}{c} 0 \\ 1 \end{array} \right] \odot \left[ \begin{array}{c} \infty \\ 0 \end{array} \right] \\ &=& \sum \left[ \begin{array}{c} 0 \\ 0 \end{array} \right] \\ &=& 0+ 0 \\ &=& 0 \end{eqnarray}

• \(\bar{y} = A \neq B\)인 경우에는 \(\mathcal{D}(\bar{y},y)\)이 커져야 한다.

\begin{eqnarray} - \sum \left[ \begin{array}{c} 0 \\ 1 \end{array} \right] \odot \log \left[ \begin{array}{c} 1 \\ 0 \end{array} \right]  &=& \sum \left[ \begin{array}{c} 0 \\ 1 \end{array} \right] \odot -\log \left[ \begin{array}{c} 1 \\ 0 \end{array} \right]  \\ &=& \sum\left[ \begin{array}{c} 0 \\ 1 \end{array} \right] \odot  \left[ \begin{array}{c} -\log 1 \\ -\log 0 \end{array} \right] \\ &=&\sum \left[ \begin{array}{c} 0 \\ 1 \end{array} \right] \odot \left[ \begin{array}{c} 0 \\ \infty \end{array} \right] \\ &=& \sum \left[ \begin{array}{c} 0 \\ \infty \end{array} \right] \\ &=& 0+ \infty \\ &=& \infty \end{eqnarray}

Logistic Cost 함수와 Cross-ENTROPY

• Logistic Cost 함수와 Cross-Entropy는 식 (3)과 같이 서로 같다.

\begin{eqnarray} C(H(x),y) &=& y\log H(x) - (1-y)\log(1-H(x)) \\ &=& -\sum_i L_i\log S_i \\ &=& \mathcal{D}(S,L) \tag{3}\end{eqnarray}

• 이유는 같은 값을 예측할 때에는 0이고, 다른 값을 예측할 때에는 \(\infty\)이기 때문이다.

• 학습 데이터가 여러 개인 경우의 Cost(Loss) 함수는 식 (4)와 같다.

\begin{array} \mahtcal{L} = \frac{1}{N} \sum_i \textrm{Cost(Loss)}(S(\mathbf{w}x_i+\mathbf{b}), L_i) \tag{4}\end{array}

Cost(Loss) 함수의 최소값을 찾는 방법

• 이전과 마찬가지로 경사하강법(Gradient Descent Algorithm)을 사용한다.

• 그림과 같이 곡선의 경사면을 따라 가면서 최소값을 찾을 수 있다.

• 어떤 점에서의 기울기는 미분계수를 구함으로써 계산할 수 있다.

• 경사면을 따라 내려가는 간격은 \(\alpha\)이며 미분계수는 식 (5)와 같다.

\begin{eqnarray} \textrm{STEP} = -\alpha \vartriangle \mathcal{L}(w_1, w_2) \tag{5} \end{eqnarray}

로지스틱 회귀 분류(Logistic Regression Classification) 연습

로지스틱 회귀 분류 모델

• 가설식(Hypothesis)

\begin{eqnarray} H(x) = \frac{1}{1+e^{-(\mathbf{W}^\intercal \mathbf{X} + \mathbf{b})}}\tag{1}\end{eqnarray}

• cost(loss) 함수

\begin{eqnarray}\textrm{cost}(W,b)=-\frac{1}{m}\sum \big( y\log H(x) + (1-y)\log (1-H(x))\big)\tag{2}\end{eqnarray}

• 경사 하강법(Gradient Descent Algorithm)
  

\begin{eqnarray}W = W - \alpha \frac{\partial}{\partial W}\textrm{cost}(W,b)\end{eqnarray}

로지스틱 회귀 분류 모델을 사용한 기계 학습 연습

• 학습에 사용할 데이터는 다음과 같다.

• \(y\) 값은 항상 0과 1을 갖는다는 것이 중요하다

• 데이터 사용 시 중요한 것은 모양(shape)이다.
  

x_data = [[1, 2], [2, 3], [3, 1], [4, 3], [5, 3], [6, 2]]
y_data = [[0], [0], [0], [1], [1], [1]]

X = tf.placeholder(tf.float32, shape=[None, 2])
Y = tf.placeholder(tf.float32, shape=[None, 1])

• 전체  코드는 다음과 같다.

import tensorflow as tf

x_data = [[1, 2], [2, 3], [3, 1], [4, 3], [5, 3], [6, 2]]
y_data = [[0], [0], [0], [1], [1], [1]]

X = tf.placeholder(tf.float32, shape=[None, 2])
Y = tf.placeholder(tf.float32, shape=[None, 1])

# weight의 shape은 X의 변수가 2개이기 때문에 [2, 1](2행 1열)이다.
W = tf.Variable(tf.random_normal([2, 1]), name='weight')
b = tf.Variable(tf.random_normal([1]), name='bias')

# 가설식
hypothesis = tf.sigmoid(tf.matmul(X, W) + b)

# cost(loss) 함수
cost = -tf.reduce_mean(Y*tf.log(hypothesis) + (1-Y)*tf.log(1-hypothesis))

# 경사 하강법
train = tf.train.GradientDescentOptimizer(learning_rate=0.01).minimize(cost)
## 여기까지가 학습을 위한 그래프를 만들었다.

## 예측한 값을 가지고 성공했는지 실피했는지 bianry 출력해야한다.
## hypothesis를 계산하면 0과 1사이의 값이기 때문에 분류의 기준을 0.5로 설정
## 0.5보다 크면 성공, 작으면 실패

# cast() 메서드를 사용하면 결과값은 0.0 또는 1.0
predicted = tf.cast(hypothesis > 0.5, dtype=tf.float32)

# 예측값과 실제값이 같은지를 확인하여 맞을 확률을 구한다
accuracy = tf.reduce_mean(tf.cast(tf.equal(predicted, Y), dtype=tf.float32))

## 이제 학습을 시키자.
# 그래프를 만든다.
with tf.Session() as sess:
    # 변수 초기화
    sess.run(tf.global_variables_initializer())

    for step in range(10001):
        cost_val, _ = sess.run([cost, train], feed_dict={X: x_data, Y: y_data})

        if step % 2000 == 0:
            print(f"STEP = {step:06}, cost 함수값= {cost_val:1.14}")

    h, c, a = sess.run([hypothesis, predicted, accuracy], feed_dict={X: x_data, Y: y_data})

    print(f"\n가설식의 값 = {h},\n실제의 값 = {c},\n정확도 = {a}")

• 결과값
  

STEP = 000000, cost 함수값= 0.53687995672226
STEP = 002000, cost 함수값= 0.3408930003643
STEP = 004000, cost 함수값= 0.25828701257706
STEP = 006000, cost 함수값= 0.20591051876545
STEP = 008000, cost 함수값= 0.17069421708584
STEP = 010000, cost 함수값= 0.14567981660366

가설식의 값 = [[ 0.0291514 ]
 [ 0.15663536]
 [ 0.29717436]
 [ 0.78491896]
 [ 0.94178247]
 [ 0.98091239]],
실제의 값 = [[ 0.]
 [ 0.]
 [ 0.]
 [ 1.]
 [ 1.]
 [ 1.]],
정확도 = 1.0

로지스틱 회귀 분류 모델을 실제 데이터에 적용하기

• 학습에 사용할 데이터는 파일로 불러온다.

• 당뇨병(diabete) 자료를 토대로 학습시켜 예측해보자.
  

import numpy as np

xy = np.loadtxt('data-03-diabetes.csv', delimiter=',', dtype=np.float32)
x_data = xy[:, 0:-1]
y_data = xy[:, [-1]]

• 나머지 학습을 위한 코드는 이전과 동일!!!

• 데이터를 불러오는 부분만 우리가 잘 설계하면 된다!!!!

• 데이터의 변수 갯수가 몇 개인지 확인한 후에 모양(shape)을 정확하게 입력해야 한다.
  

import tensorflow as tf
import numpy as np

xy = np.loadtxt('data-03-diabetes.csv', delimiter=',', dtype=np.float32)
x_data = xy[:, 0:-1]
y_data = xy[:, [-1]]

X = tf.placeholder(tf.float32, shape=[None, 8])
Y = tf.placeholder(tf.float32, shape=[None, 1])

W = tf.Variable(tf.random_normal([8, 1]), name='weight')
b = tf.Variable(tf.random_normal([1]), name='bias')

hypothesis = tf.sigmoid(tf.matmul(X, W) + b)

cost = -tf.reduce_mean(Y*tf.log(hypothesis) + (1-Y)*tf.log(1-hypothesis))
train = tf.train.GradientDescentOptimizer(learning_rate=0.01).minimize(cost)

predicted = tf.cast(hypothesis > 0.5, dtype=tf.float32)
accuracy = tf.reduce_mean(tf.cast(tf.equal(predicted, Y), dtype=tf.float32))

with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())

    feed = {X: x_data, Y: y_data}

    for step in range(10001):
        sess.run(train, feed_dict=feed)
        if step % 2000 == 0:
            print(f"STEP = {step:06}, cost 합수값 = {sess.run(cost, feed_dict=feed)}")

    h, c, a = sess.run([hypothesis, predicted, accuracy], feed_dict=feed)
    print(f"\n가설식의 값 = {h},\n\n실제의 값 = {c},\n\n정확도 = {a}")

STEP = 000000, cost 합수값 = 1.585148811340332
STEP = 002000, cost 합수값 = 0.5984190106391907
STEP = 004000, cost 합수값 = 0.5360344648361206
STEP = 006000, cost 합수값 = 0.5096880793571472
STEP = 008000, cost 합수값 = 0.4965749979019165
STEP = 010000, cost 합수값 = 0.48917973041534424

가설식의 값 = [[ 0.43279484]
 [ 0.92194134]
 [ 0.15470713]
 [ 0.93848407]
...
 [ 0.72711807]
 [ 0.75625086]
 [ 0.78592217]
 [ 0.69465518]
 [ 0.8947171 ]],

실제의 값 = [[ 0.]
 [ 1.]
 [ 0.]
 [ 1.]
 [ 0.]
...
 [ 1.]
 [ 1.]
 [ 1.]
 [ 1.]
 [ 1.]
 [ 1.]],

정확도 = 0.7628458738327026

로지스틱  회귀 분류(Logistic regression classification)

로지스틱 회귀를 이용한 대상 분류 방법

• 분류 알고리즘(classification algorithm) 중에서 굉장히 정확도가 높은 모델로 알려져 있음

• 바로 실제 문제에 적용이 가능

• 뉴럴 네트워크와 딥 러닝의 중요한 요소임

선형 회귀 분석 되돌아보기

• 아래 표와 같은 데이터에 대하여 회귀 분석을 해보자.

• 시간(\(x_1\))과 참석 횟수(\(x_2\))를 가지고 시험 성적(\(y\))을 예측하려고 한다.
• 시험 성적을 예측하는 것이 회귀 분석(regression)이다.
  

• 선형 회귀 분석(Linear Regression Analysis) 방법
1. 가설식(hypothesis)을 만든다. \(H(\mathbf{X})=\mathbf{X}\mathbf{W} + \mathbf{b}\)
1. cost(loss) 함수를 계산한다. \(\textrm{cost(loss)}(\mathbf{W}, \mathbf{b})=\frac{1}{m}\sum_{i=1}^m((\mathbf{W}\mathbf{X} - \mathbf{b} ) - \mathbf{Y})^2\)
2. cost(loss) 함수가 최소가 되는 weight와 bias를 경사 하강법으로 찾는다. $$W=W-\alpha\frac{\partial}{\partial W}\textrm{cost(loss)}$$

분류(classification) 문제

• 스팸 메일 탐지(spam mail detection) : 스팸(spam) 또는 정상(ham)

• 페이스북 피드(facebook feed) : 친구들이 작성한 글을 타임라인에서 보여주기(show) 또는 감추기(hide)

• 이전에 '좋아요'를 눌렀던 글을 참고로 해서 보여줄지 말지를 결정

• 신용카드 비정상 거래 탐지(credit card fraudulent transaction detection) : 정상 거래(legitimate) 또는 비정상 거래(fraud)

• 이전에 사용했던 거래내역들의 형태를 보고 탐지

분류(classification) 문제를 기계적으로 학습을 시켜보자

• 분류 문제를 기계적으로 학습시키기 위해서는 분류 대상(category)을 '0'과 '1'으로 인코딩한다!
  

• 스팸(1) 또는 정상(0)

• 보여주기(1) 또는 감추기(0)
  

• 정상 거래(0) 또는 비정상 거래(1)

• 최근들어서는 굉장히 많은 곳에서 사용하기 때문에 중요!!
  

• 의료용 사진 판독 : 양성 종양인지 악성 종양인지 분류

• 주식 거래 : 이전의 주식 매매 패턴을 학습하여 살건지 팔건지 판단

로지스틱 회귀 분석 개념

• 공부한 시간을 토대로 시험에 합격(1)할 것인지 불합격(0)할 것인지 분류해보자.

• 합격/불합격 2가지로 분류(binary classification)하는 문제
  

• 선형 회귀 모델로 분석한다고 해보자.

• 선형 회귀 모델(\(H(x)=Wx+b\))을 만들면 아래 그림처럼 직선이 만들어진다.
  

• 0.5를 잡아서 왼쪽에 있으면 불합격, 오른쪽에 있으면 합격으로 분류할 수 있다.
  

• 그러나 이 모델은 문제가 있다!!!

• 예를 들어 50시간을 공부한 사람이 있다고 해보자.

• 일반 선형 모델에서는 50시간을 공부하면 결과값이 높게 나타날 것이지만 결과는 0과 1로 2가지이기 때문에  50시간을 공부한 사람의 값은 1이기 때문에 그래프 아래에 놓이게 된다.

• 이 사람에 맞춰서 다시 모델을 그리게 되면 기울기가 더 낮아지는 그래프가 그려질 수 밖에 없다.

• 0.5의 점선을 더 오른쪽으로 늘려보면 어떤 사람들은 기준보다 낮아져서 불합격으로 처리될 수 있다.

• 또 다른 문제

• 우리는 \(y\)의 값이 0 또는 1이라는 것을 알고있다. 그러나 가설식 \(H(x)=Wx+b\)는 0보다 작거나 1보다 클 수가 있다.

• 예를 들어, 데이터 \(\mathbf{x}=[1, 2, 5, 10, 11]\)을 가지고 학습을 통해 \(W=0.5\), \(b=0\)이라는 값을 얻었다고 해보자. 그러면 결과값은 \(0<H(x)<1\)이 될 것이다.

• 이 모델로 100시간을 공부한 사람을 모델에 적용해보자. \(H(100)=0.5\times 100=50\)이 나온다. 1보다 엄청 크기 때문에 모양이 좋지 않다.

• 따라서 우리는 결과값이 0부터 1사이에 있는 새로운 함수를 찾아야만 한다. 그래서 찾은 것이 sigmoid 또는 logistic 함수 \(g(z)\)(식 (1))이다.
  

\begin{eqnarray}g(z)=\frac{1}{1+e^{-z}}\tag{1}\end{eqnarray}

로지스틱 회귀 분류 모델

• 가설식(Hypothesis)
  

• 이제 우리는 \(z=Wx+b\)라고 하고, 가설식을 \(H(x) = g(z)\)로 하면 된다. 그러면 로지스틱 회귀 모델의 가설식은 식 (2)와 같다.
  

\begin{eqnarray}H(\mathbf{X})=\frac{1}{1+e^{-(\mathbf{W}^\intercal\mathbf{X}+\mathbf{b})}}\tag{2}\end{eqnarray}

• cost(loss) 함수

• 선형 모델 \(H(x)=Wx+b\)일 때의 cost(loss) 함수는 식 (3)과 같으며 이를 그래프로 표현하면 아래 그림과 같다.

• 이 cost(loss) 함수의 장점은 경사 하강법을 사용할 때 어느 점에서 시작하던지 우리는 항상 최저점에 도달할 수 있다는 것이다.
  

\begin{eqnarray}\textrm{cost}(W,b)=\frac{1}{m}\sum_{i=1}^m\big(H(x_i) -y_i\big)^2\end{eqnarray}

• 그러나 로지스틱 회귀 분류 모델에서는 sigmoid 함수를 사용하기 때문에 가설식이 식 (2)처럼 된다. cost(loss) 함수의 그래프를 그려보면 아래 그림과 같이 구불구불하게 그려진다.
  

• 선형 모델에서는 어느 점에서 시작하던지 경사 하강법으로 최저점에 도달할 수 있다.

• 로지스틱 모델에서는 시작하는 점에 따라서 극소점이 달라지기 때문에 최저점에 도달하는 것이 어렵다. 그래서 cost(loss) 함수도 변형해야만 한다.

• 로지스틱 회귀 분류 모델의 cost(loss) 함수는 식 (3)과 같다.

\begin{eqnarray}\textrm{cost}(W,b)=\frac{1}{m}\sum\mathfrak{c}(H(x),y)\tag{3}\end{eqnarray}

\begin{eqnarray}\mathfrak{c}\left(H\left(x\right), y\right)=\left\{\begin{array}{ll}-\log H(x) &\textrm{if $y=1$}\\-\log(1-H(x))&\textrm{if $y=0$}\end{array}\right.\tag{4}\end{eqnarray}

• cost(loss) 함수의 의미는 실제의 값과 예측한 값이 같으면 작아지고, 다르면 값이 커지도록 하는 것이다. 이렇게 되도록 가설식의 weight와 bias를 조정하는 것이다.
  

• 이제 \(y=1\)일 때를 생각해보자.

• 예측값이 \(H(x)=1\)로 맞았을 때의 cost(loss) 함수값을 계산해보자.

• cost(loss) 함수는 \(g(z)=-\log z\)이기 때문에 \(\textrm{cost}(1)=-\log 1=0\)이다.
  

• 예측값이 \(H(x)=0\)으로 틀렸을 때의 cost(loss) 함수값을 계산해보자.

• cost(loss) 함수는 \(g(z)=-\log z\)이기 때문에 \(\textrm{cost}(0)=-\log 0=\infty\)로 값이 커져 벌을 줄 수가 있다.

• 이제 \(y=0\)일 때를 생각해보자.

• 예측값이 \(H(x)=0\)으로 맞았을 때의 cost(loss) 함수값을 계산해보자.

• cost(loss) 함수는 \(g(z)=-\log(1- z)\)이기 때문에 \(\textrm{cost}(1)=-\log (1-0)=-\log 1=0\)이다.

• 예측값이 \(H(x)=1\)로 틀렸을 때의 cost(loss) 함수값을 계산해보자.

• cost(loss) 함수는 \(g(z)=-\log (1-z)\)이기 때문에 \(\textrm{cost}(1)=-\log (1-1)=-\log 0=\infty\)로 값이 커져 벌을 줄 수가 있다.

• 이 새로운 cost(loss) 함수의 2가지 경우의 그래프를 결합하면 우리가 원하는 convex 함수를 만들 수 있게 되는 것이다.

• \(\mathfrak{c}(H(x),y)\) 함수는 식 (4)처럼  \(y\) 값에 따른 if 조건문이 있기 때문에 코딩하려면 힘이든다. 그래서 코딩하기 쉽도록 if 조건문이 없는 형태로 정의하면 식 (5)와 같으며, \(y\) 값에 따라 식을 전개를 해보면 식 (5)는 식 (4)와 같다는 것을 알 수 있다.
  

\begin{eqnarray} \mathfrak{c}(H(x),y)&=&-y\log H(x)-(1-y)\log(1-H(x))\tag{5}\\&=&\left\{\begin{array}{ll}-1\times \log H(x) - (1-1)\times \log (1-H(x) )&\textrm{if \(y=1\)}\\-0\times \log H(x) - (1-0)\times \log(1-H(x))&\textrm{if \(y=0\)}\end{array}\right.\\&=&\left\{\begin{array}{ll}- \log H(x) - 0\times \log (1-H(x)) &\textrm{if \(y=1\)}\\- 1\times \log(1-H(x))&\textrm{if \(y=0\)}\end{array}\right.\\&=&\left\{\begin{array}{ll}- \log H(x) &\textrm{if \(y=1\)}\\- \log(1-H(x))&\textrm{if \(y=0\)}\end{array}\right.\end{eqnarray}

• 최종적으로 cost(loss) 함수는 식 (6)과 같다.

\begin{eqnarray}\textrm{cost}(W) = -\frac{1}{m}\sum_{i=1}^m\big(y_i\log H(x_i)+(1-y)\log (1-H(x_i))\big)\tag{6}\end{eqnarray}

• 경사 하강법(Gradient Descent Algorithm)
  

• 이제 cost(loss) 함수 식 (6)의 최소값을 구하기 위해 경사 하강법을 사용해보자.

• 기울기를 구하기 위해 식 (6)을 식 (7)과 같이 미분한다.

• 식 (7)을 계산하는 것은 복잡하다. 그러나 컴퓨터가 알아서 해주니 개념만 알고 있으면 된다.
  

\begin{eqnarray}W=W-\alpha\frac{\partial}{\partial W}\textrm{cost}(W)\tag{7}\end{eqnarray}

• 식 (6)의 코드는 다음과 같다.

import tensorflow as tf

# cost(loss) 함수
cost = -tf.reduce_mean(Y*tf.log(hypothesis) + (1-Y)*tf.log(1-hypothesis))

• 식 (7)의 코드는 다음과 같다.
  

import tensorflow as tf

# 경사 하강법
a = tf.Variable(0.1) # learning rate = alpha
optimizer = tf.train.GradientDescentOptimizer(a)
train = optimizer.minimize(cost)

다변수 선형 회귀(Multi-variable Linear Regression) 연습

변수가 3개인 아래의 표를 텐서플로우로 구현하기

• 아래의 표에 대하여 가설식은 다음과 같이 쓸 수 있다.

\begin{equation} H(x_1, x_2, x_3) = x_1\times w_1 + x_2\times w_2 + x_3 \times x_3 + b\tag{1}\end{equation}

• 가설식과 훈련용 데이터는 텐서플로우를 사용하여 다음과 같이 구현한다.

• 변수가 1개일 때 구현했던 코드의 방식으로 구현
  

# 훈련용 데이터 입력
x1_data = [ 73.,  93.,  89.,  96.,  73.]
x2_data = [ 80.,  88.,  91.,  98.,  66.]
x3_data = [ 75.,  93.,  90., 100.,  70.]
y_data  = [152., 185., 180., 196., 142.]

# plaeceholder를 사용하여 텐서 자료를 입력
x1 = tf.placeholder(tf.float32)
x2 = tf.placeholder(tf.float32)
x3 = tf.placeholder(tf.float32)

Y = tf.placeholder(tf.float32)

# weight와 bias는 난수를 발생하여 조정을 하는 값이기에 변수로 설정하며, 모양(shape)은 1차원 벡터
w1 = tf.Variable(tf.random_normal([1]), name='weight1')
w2 = tf.Variable(tf.random_normal([1]), name='weight2')
w3 = tf.Variable(tf.random_normal([1]), name='weight3')
b = tf.Variable(tf.random_normal([1]), name='bias')

# 가설식은 식(1)과 같이 입력
hypothesis = x1*w1 + x2*w2 + x3*w3 + b

• 텐서플로우 그래프로 구현을 위한 전체 코드

import tensorflow as tf

# 훈련용 데이터 입력
x1_data = [ 73.,  93.,  89.,  96.,  73.]
x2_data = [ 80.,  88.,  91.,  98.,  66.]
x3_data = [ 75.,  93.,  90., 100.,  70.]
y_data  = [152., 185., 180., 196., 142.]

# plaeceholder를 사용하여 텐서 자료를 입력
x1 = tf.placeholder(tf.float32)
x2 = tf.placeholder(tf.float32)
x3 = tf.placeholder(tf.float32)

Y = tf.placeholder(tf.float32)

# weight와 bias는 난수를 발생하여 조정을 하는 값이기에 변수로 설정하고, 모양(shape)은 1차원 벡터
w1 = tf.Variable(tf.random_normal([1]), name='weight1')
w2 = tf.Variable(tf.random_normal([1]), name='weight2')
w3 = tf.Variable(tf.random_normal([1]), name='weight3')
b = tf.Variable(tf.random_normal([1]), name='bias')

# 가설식을 세운다.
hypothesis = x1*w1 + x2*w2 + x3*w3 + b

# cost(loss) 함수
cost = tf.reduce_mean(tf.square(hypothesis - Y))

# 데이터에 대하여 cost 함수의 극소값을 구하기 위하여 경사 하강법 최적화 메서드를 사용
optimizer = tf.train.GradientDescentOptimizer(learning_rate=1e-5)

# cost 함수에 대하여 경사 하강법으로 극소값 구하기
train = optimizer.minimize(cost)

# 세션에서 그래프 만들기
sess = tf.Session()

# 변수 초기화
sess.run(tf.global_variables_initializer())

# 학습은 2000번을 시킴
for step in range(2001):
    
#sess.run() 메서드로 그래프를 실행하고 placeholder를 위해 feed_dict으로 데이터 입력
    cost_val, hy_val, _ = sess.run([cost, hypothesis, train],
                                   feed_dict={x1: x1_data, x2: x2_data, x3: x3_data, Y: y_data})

# 10번마다 출력
    if step % 10 == 0:
        print(f"STEP = {step:04}, cost = {cost_val:>2.2}, 예측값 = {hy_val}")

• 실행 결과 1: 실행할 때마다 2000번 학습 후의 cost(loss) 함수 극소값이 변한다.

STEP = 0000, cost = 1.7e+05, 예측값 = [-220.54341125 -247.40852356 -252.95663452 -274.93395996 -184.68412781]
STEP = 0100, cost = 2.9e+01, 예측값 = [ 143.69319153  189.97506714  178.21386719  194.57540894  148.8497467 ]
STEP = 0200, cost = 2.8e+01, 예측값 = [ 143.90032959  189.83311462  178.27740479  194.62081909  148.66397095]
STEP = 0300, cost = 2.6e+01, 예측값 = [ 144.10192871  189.69499207  178.33926392  194.66497803  148.48318481]
STEP = 0400, cost = 2.5e+01, 예측값 = [ 144.29812622  189.56054688  178.39944458  194.70794678  148.30722046]
STEP = 0500, cost = 2.4e+01, 예측값 = [ 144.48912048  189.42965698  178.45803833  194.74975586  148.13598633]
STEP = 0600, cost = 2.2e+01, 예측값 = [ 144.67500305  189.30229187  178.51507568  194.79043579  147.96931458]
STEP = 0700, cost = 2.1e+01, 예측값 = [ 144.855896    189.17831421  178.57055664  194.82998657  147.80711365]
STEP = 0800, cost = 2e+01, 예측값 = [ 145.03199768  189.05767822  178.62460327  194.86851501  147.64927673]
STEP = 0900, cost = 1.9e+01, 예측값 = [ 145.2033844   188.94024658  178.67718506  194.90597534  147.4956665 ]
STEP = 1000, cost = 1.8e+01, 예측값 = [ 145.37019348  188.82594299  178.7283783   194.94242859  147.34616089]
STEP = 1100, cost = 1.7e+01, 예측값 = [ 145.532547    188.71469116  178.77818298  194.97789001  147.20066833]
STEP = 1200, cost = 1.6e+01, 예측값 = [ 145.69056702  188.60643005  178.82667542  195.01239014  147.05905151]
STEP = 1300, cost = 1.5e+01, 예측값 = [ 145.84437561  188.50105286  178.87388611  195.04597473  146.92124939]
STEP = 1400, cost = 1.5e+01, 예측값 = [ 145.99407959  188.39846802  178.91981506  195.07861328  146.78713989]
STEP = 1500, cost = 1.4e+01, 예측값 = [ 146.13977051  188.29864502  178.96453857  195.1104126   146.65663147]
STEP = 1600, cost = 1.3e+01, 예측값 = [ 146.28160095  188.20149231  179.00805664  195.14131165  146.52960205]
STEP = 1700, cost = 1.2e+01, 예측값 = [ 146.4196167   188.10691833  179.0504303   195.17140198  146.4059906 ]
STEP = 1800, cost = 1.2e+01, 예측값 = [ 146.55397034  188.01487732  179.09165955  195.20066833  146.28567505]
STEP = 1900, cost = 1.1e+01, 예측값 = [ 146.68473816  187.92527771  179.13179016  195.22911072  146.16860962]
STEP = 2000, cost = 1.1e+01, 예측값 = [ 146.81201172  187.83810425  179.17086792  195.25683594  146.05465698]

• 실행 결과 2
  

STEP = 0000, cost = 1.1e+05, 예측값 = [-136.4148407  -163.72163391 -161.54948425 -175.06773376 -125.43991089]
STEP = 0100, cost = 2.2, 예측값 = [ 152.6002655   183.7406311   180.76570129  197.70622253  139.60707092]
STEP = 0200, cost = 2.2, 예측값 = [ 152.55526733  183.77182007  180.75238037  197.69287109  139.65115356]
STEP = 0300, cost = 2.1, 예측값 = [ 152.51152039  183.80220032  180.73945618  197.67982483  139.69410706]
STEP = 0400, cost = 2.0, 예측값 = [ 152.46899414  183.83172607  180.72689819  197.66705322  139.73597717]
STEP = 0500, cost = 1.9, 예측값 = [ 152.42764282  183.86042786  180.71470642  197.65457153  139.77677917]
STEP = 0600, cost = 1.9, 예측값 = [ 152.38745117  183.88838196  180.7028656   197.64233398  139.81652832]
STEP = 0700, cost = 1.8, 예측값 = [ 152.34835815  183.9155426   180.69134521  197.63034058  139.85525513]
STEP = 0800, cost = 1.7, 예측값 = [ 152.31034851  183.94197083  180.68016052  197.61860657  139.89302063]
STEP = 0900, cost = 1.7, 예측값 = [ 152.27339172  183.96765137  180.66931152  197.6071167   139.92982483]
STEP = 1000, cost = 1.6, 예측값 = [ 152.23748779  183.99264526  180.65878296  197.59585571  139.96568298]
STEP = 1100, cost = 1.6, 예측값 = [ 152.20256042  184.01695251  180.64852905  197.58483887  140.00062561]
STEP = 1200, cost = 1.5, 예측값 = [ 152.16860962  184.04057312  180.63859558  197.57402039  140.03469849]
STEP = 1300, cost = 1.5, 예측값 = [ 152.13563538  184.06358337  180.62895203  197.56344604  140.06791687]
STEP = 1400, cost = 1.5, 예측값 = [ 152.1035614   184.08592224  180.61958313  197.55307007  140.1002655 ]
STEP = 1500, cost = 1.4, 예측값 = [ 152.07237244  184.10765076  180.61048889  197.54292297  140.13182068]
STEP = 1600, cost = 1.4, 예측값 = [ 152.04206848  184.12879944  180.60166931  197.53294373  140.16259766]
STEP = 1700, cost = 1.3, 예측값 = [ 152.01261902  184.14935303  180.59310913  197.52319336  140.19258118]
STEP = 1800, cost = 1.3, 예측값 = [ 151.98400879  184.16934204  180.58480835  197.5136261   140.22181702]
STEP = 1900, cost = 1.3, 예측값 = [ 151.95617676  184.18875122  180.57672119  197.50421143  140.25030518]
STEP = 2000, cost = 1.2, 예측값 = [ 151.92913818  184.2076416   180.56889343  197.49502563  140.27810669]

• 실행 결과 3

STEP = 0000, cost = 3.9e+04, 예측값 = [-18.12299919 -29.6329422  -25.06500816 -28.79134178 -23.24040413]
STEP = 0100, cost = 1.3e+01, 예측값 = [ 156.88265991  180.98231506  182.31651306  197.05860901  137.4597168 ]
STEP = 0200, cost = 1.3e+01, 예측값 = [ 156.74263     181.07827759  182.27355957  197.02807617  137.58518982]
STEP = 0300, cost = 1.2e+01, 예측값 = [ 156.60632324  181.17166138  182.23170471  196.99833679  137.70729065]
STEP = 0400, cost = 1.1e+01, 예측값 = [ 156.47367859  181.26254272  182.19100952  196.96942139  137.8261261 ]
STEP = 0500, cost = 1.1e+01, 예측값 = [ 156.34454346  181.35101318  182.15135193  196.94128418  137.94177246]
STEP = 0600, cost = 1e+01, 예측값 = [ 156.21887207  181.43711853  182.11277771  196.91392517  138.05430603]
STEP = 0700, cost = 9.7, 예측값 = [ 156.09654236  181.5209198   182.07521057  196.88728333  138.16383362]
STEP = 0800, cost = 9.2, 예측값 = [ 155.97747803  181.60247803  182.03865051  196.86135864  138.27043152]
STEP = 0900, cost = 8.8, 예측값 = [ 155.86161804  181.68186951  182.00309753  196.8361969   138.37416077]
STEP = 1000, cost = 8.3, 예측값 = [ 155.74882507  181.75914001  181.96846008  196.81164551  138.47512817]
STEP = 1100, cost = 7.9, 예측값 = [ 155.63903809  181.83433533  181.93473816  196.78781128  138.57337952]
STEP = 1200, cost = 7.5, 예측값 = [ 155.53219604  181.907547    181.90193176  196.7645874   138.66897583]
STEP = 1300, cost = 7.1, 예측값 = [ 155.42819214  181.97877502  181.87001038  196.74201965  138.76203918]
STEP = 1400, cost = 6.7, 예측값 = [ 155.32696533  182.04811096  181.83891296  196.72007751  138.85258484]
STEP = 1500, cost = 6.4, 예측값 = [ 155.22842407  182.11561584  181.80865479  196.69869995  138.9407196 ]
STEP = 1600, cost = 6.0, 예측값 = [ 155.13253784  182.18130493  181.77920532  196.67791748  139.026474  ]
STEP = 1700, cost = 5.7, 예측값 = [ 155.03919983  182.24523926  181.75053406  196.6577301   139.10993958]
STEP = 1800, cost = 5.4, 예측값 = [ 154.94836426  182.3074646   181.72262573  196.63806152  139.19116211]
STEP = 1900, cost = 5.2, 예측값 = [ 154.85992432  182.36802673  181.69544983  196.61891174  139.27020264]
STEP = 2000, cost = 4.9, 예측값 = [ 154.77386475  182.42698669  181.66902161  196.60032654  139.34713745]

변수가 3개 데이터를 행렬식을 이용하여 텐서플로우로 구현하기

• 위의 식 (1)을 행렬식으로 표현하면 다음과 같이 쓸 수 있다.

\begin{eqnarray}(x_1, x_2, x_3) \cdot \left(\begin{array}{c} w_1\\ w_2\\ w_3\end{array}\right) + b = (x_1 w_1 + x_2 w_2 + x_3 w_3 + b)\tag{2}\end{eqnarray}

$$H(\mathbf{X}) = \mathbf{X}\cdot\mathbf{W} + b$$

• 식 (2)를 코드로 구현하면 다음과 같다.
• 행렬식을 이용하면 데이터 선언부의 코드가 간결해진다.
  

import tensorflow as tf

# 인스턴스 데이터
x_data = [[73., 80., 75.], [93., 88., 93.], [89., 91., 90.],
          [96., 98., 100.], [73., 66., 70]]
y_data = [[152.], [185.], [180.], [196.], [142.]]

# placeholder를 사용하여 텐서 자료를 입력
# 예에서 X의 차원은 5x3이지만 인스턴스의 갯수는 얼마인지 모르기 때문에 None으로 설정
# 에어서 Y의 차원은 5x1이지만 인스턴스의 갯수는 얼마인지 모르기 때문에 None으로 설정
X = tf.placeholder(tf.float32, shape=[None, 3])
Y = tf.placeholder(tf.float32, shape=[None, 1])

# weight와 bias는 난수를 발생하여 조정을 하는 값이기에 변수로 설정하고, 모양(shape)은 1차원 벡터
W = tf.Variable(tf.random_normal([3, 1]), name='weight')
b = tf.Variable(tf.random_normal([1]), name='bias')

# 가설식은 다음과 같이 구현
hypothesis = tf.matmul(X, W) + b

# cost(loss) 함수
cost = tf.reduce_mean(tf.square(hypothesis - Y))

# cost 함수의 극소값을 경사 하강법으로 계산
optimizer = tf.train.GradientDescentOptimizer(learning_rate=1e-5)
train = optimizer.minimize(cost)

# 세션에서 그래프 만들기
sess = tf.Session()
sess.run(tf.global_variables_initializer())

for step in range(20001):
    cost_val, hy_val, _ = sess.run([cost, hypothesis, train],
                                    feed_dict={X: x_data, Y: y_data})
    if step % 5000 == 0:
        print(f"STEP = {step:06}, cost = {cost_val:>2.2}, \n\t예측값 = {hy_val}")

• 실행 결과
  

STEP = 000000, cost = 1.3e+05, 
	예측값 = [[-165.87182617]
 [-201.77796936]
 [-197.4772644 ]
 [-213.77851868]
 [-155.99333191]]
STEP = 005000, cost = 1.8, 
	예측값 = [[ 151.40869141]
 [ 184.49110413]
 [ 180.5823822 ]
 [ 197.92095947]
 [ 139.85758972]]
STEP = 010000, cost = 1.2, 
	예측값 = [[ 150.81903076]
 [ 184.91998291]
 [ 180.43295288]
 [ 197.56921387]
 [ 140.62631226]]
STEP = 015000, cost = 0.96, 
	예측값 = [[ 150.73706055]
 [ 184.99801636]
 [ 180.43545532]
 [ 197.35534668]
 [ 140.91104126]]
STEP = 020000, cost = 0.8, 
	예측값 = [[ 150.77804565]
 [ 184.98928833]
 [ 180.47247314]
 [ 197.19113159]
 [ 141.06103516]]

파일에서 데이터를 불러와 학습시키기

• .csv 파일로 저장된 데이터를 읽기 위해서 numpy 모듈의 loadtxt() 메서드를 사용

import numpy as np
import tensorflow as tf
tf.set_random_seed(777) # 난수발생의 초기값을 주면 실행할 때마다 같은 결과가 나온다.

# 텍스트 파일 불러오기
xy = np.loadtxt('data-01-test-score.csv', delimiter=',', dtype=np.float32)

# 모든 데이터 행과 처음부터 마지막 -1개의 열까지 선택
x_data = xy[:, 0:-1]
# 마지막 열만 선택
y_data = xy[:, [-1]]

# 데이터가 정상적으로 들어왔는지 확인
print(x_data.shape, x_data, len(x_data))
print(y_data.shape, y_data)

# 학습을 위한 데이터는 실행 시 입
X = tf.placeholder(tf.float32, shape=[None, 3])
Y = tf.placeholder(tf.float32, shape=[None, 1])

W = tf.Variable(tf.random_normal([3, 1]), name='weight')
b = tf.Variable(tf.random_normal([1]), name='bias')

# 가설식
hypothesis = tf.matmul(X, W) + b

# cost(loss) 함수
cost = tf.reduce_mean(tf.square(hypothesis - Y))

# 경사 하강법
optimizer = tf.train.GradientDescentOptimizer(learning_rate=1e-5)
train = optimizer.minimize(cost)

sess = tf.Session()

# 변수 초기화
sess.run(tf.global_variables_initializer())

for step in range(2001):
    cost_val, hy_val, _ = sess.run([cost, hypothesis, train], feed_dict={X: x_data, Y: y_data})

    if step % 100 == 0:
        print(f"STEP = {step:06}, cost = {cost_val:>2.2}, 예측값 = {hy_val}")

print(f"예상 점수는 {sess.run(hypothesis, feed_dict={X: [[100, 70, 101]]})}점입니다.")
print(f"예상 점수는 {sess.run(hypothesis, feed_dict={X: [[60, 70, 110], [90, 100, 80]]})}입니다.")

• 실행 결과
  

STEP = 000000, cost = 2.1e+04, 예측값 = [[ 22.04806328]
 [ 21.61978722]
 [ 24.09669304]
 [ 22.29300499]
 [ 18.6339016 ]
 [  7.2669735 ]
 [ 12.33102989]
 [  3.15051103]
 [ 14.34794426]
 [  4.25342369]
 [ 14.48570824]
 [ 10.67806816]
 [ 28.80463982]
 [ 29.29880333]
 [ 11.23783684]
 [ 18.6465435 ]
 [ 31.18945122]
 [ 13.34466362]
 [ 28.84174156]
 [ 25.66280937]
 [ 15.08476067]
 [ 16.79836845]
 [ 15.92455101]
 [ 31.36112022]
 [ 24.98636436]]
STEP = 000100, cost = 8.9e+01, 예측값 = [[ 157.79551697]
 [ 185.16719055]
 [ 185.02406311]
 [ 197.75952148]
 [ 143.29411316]
 [  99.53504944]
 [ 143.86805725]
 [ 100.9239502 ]
 [ 167.53520203]
 [ 146.62893677]
 [ 141.12159729]
 [ 135.79484558]
 [ 194.86228943]
 [ 167.07516479]
 [ 143.46055603]
 [ 184.7673645 ]
 [ 162.27658081]
 [ 171.24031067]
 [ 187.06117249]
 [ 167.22627258]
 [ 169.31620789]
 [ 170.40232849]
 [ 162.88063049]
 [ 167.75440979]
 [ 194.32646179]]
STEP = 000200, cost = 8.2e+01, 예측값 = [[ 157.52545166]
 [ 185.21311951]
 [ 184.86227417]
 [ 197.77949524]
 [ 143.25938416]
 [  99.85552216]
 [ 144.07087708]
 [ 101.32597351]
 [ 167.90383911]
 [ 147.4372406 ]
 [ 141.22596741]
 [ 136.13650513]
 [ 194.50056458]
 [ 166.51863098]
 [ 143.74137878]
 [ 184.96679688]
 [ 161.62319946]
 [ 171.52180481]
 [ 186.62805176]
 [ 166.83427429]
 [ 169.53741455]
 [ 170.61328125]
 [ 163.00415039]
 [ 167.02830505]
 [ 194.22337341]]
STEP = 000300, cost = 7.6e+01, 예측값 = [[ 157.26860046]
 [ 185.25523376]
 [ 184.70755005]
 [ 197.79917908]
 [ 143.22341919]
 [ 100.16048431]
 [ 144.26712036]
 [ 101.71485138]
 [ 168.25456238]
 [ 148.20953369]
 [ 141.3263092 ]
 [ 136.46244812]
 [ 194.15400696]
 [ 165.98475647]
 [ 144.01177979]
 [ 185.15658569]
 [ 160.99502563]
 [ 171.79490662]
 [ 186.21368408]
 [ 166.4597168 ]
 [ 169.75090027]
 [ 170.81416321]
 [ 163.12428284]
 [ 166.33384705]
 [ 194.12316895]]
STEP = 000400, cost = 7.1e+01, 예측값 = [[ 157.02441406]
 [ 185.29376221]
 [ 184.55958557]
 [ 197.818573  ]
 [ 143.18641663]
 [ 100.45061493]
 [ 144.45703125]
 [ 102.09101868]
 [ 168.58824158]
 [ 148.94743347]
 [ 141.4228363 ]
 [ 136.77339172]
 [ 193.82192993]
 [ 165.47264099]
 [ 144.2721405 ]
 [ 185.33714294]
 [ 160.39103699]
 [ 172.05995178]
 [ 185.81723022]
 [ 166.10186768]
 [ 169.95700073]
 [ 171.00540161]
 [ 163.24116516]
 [ 165.66970825]
 [ 194.02583313]]
STEP = 000500, cost = 6.6e+01, 예측값 = [[ 156.79225159]
 [ 185.3289032 ]
 [ 184.41809082]
 [ 197.837677  ]
 [ 143.14839172]
 [ 100.72661591]
 [ 144.64083862]
 [ 102.45493317]
 [ 168.90560913]
 [ 149.65238953]
 [ 141.51565552]
 [ 137.06997681]
 [ 193.50372314]
 [ 164.9813385 ]
 [ 144.52288818]
 [ 185.50892639]
 [ 159.81025696]
 [ 172.31713867]
 [ 185.4379425 ]
 [ 165.75994873]
 [ 170.15597534]
 [ 171.18740845]
 [ 163.35482788]
 [ 165.03453064]
 [ 193.93121338]]
STEP = 000600, cost = 6.1e+01, 예측값 = [[ 156.57159424]
 [ 185.36087036]
 [ 184.28277588]
 [ 197.85649109]
 [ 143.10952759]
 [ 100.989151  ]
 [ 144.81872559]
 [ 102.80702209]
 [ 169.2074585 ]
 [ 150.32595825]
 [ 141.60496521]
 [ 137.35290527]
 [ 193.19885254]
 [ 164.51004028]
 [ 144.76437378]
 [ 185.67233276]
 [ 159.2517395 ]
 [ 172.56677246]
 [ 185.07507324]
 [ 165.43330383]
 [ 170.3480835 ]
 [ 171.36068726]
 [ 163.46540833]
 [ 164.42706299]
 [ 193.83927917]]
STEP = 000700, cost = 5.7e+01, 예측값 = [[ 156.36187744]
 [ 185.38980103]
 [ 184.15339661]
 [ 197.87501526]
 [ 143.06987   ]
 [ 101.23881531]
 [ 144.99092102]
 [ 103.14772034]
 [ 169.49452209]
 [ 150.96943665]
 [ 141.69085693]
 [ 137.62275696]
 [ 192.90667725]
 [ 164.05786133]
 [ 144.99700928]
 [ 185.82775879]
 [ 158.71463013]
 [ 172.80905151]
 [ 184.72793579]
 [ 165.12123108]
 [ 170.53359985]
 [ 171.52554321]
 [ 163.57298279]
 [ 163.84609985]
 [ 193.74992371]]
STEP = 000800, cost = 5.3e+01, 예측값 = [[ 156.16262817]
 [ 185.4158783 ]
 [ 184.0296936 ]
 [ 197.89324951]
 [ 143.02955627]
 [ 101.47621155]
 [ 145.15762329]
 [ 103.47737885]
 [ 169.76745605]
 [ 151.584198  ]
 [ 141.77349854]
 [ 137.88009644]
 [ 192.62672424]
 [ 163.6240387 ]
 [ 145.22106934]
 [ 185.97554016]
 [ 158.19802856]
 [ 173.04420471]
 [ 184.39579773]
 [ 164.82312012]
 [ 170.7127533 ]
 [ 171.68243408]
 [ 163.67765808]
 [ 163.29051208]
 [ 193.66308594]]
STEP = 000900, cost = 5e+01, 예측값 = [[ 155.97331238]
 [ 185.43925476]
 [ 183.91137695]
 [ 197.91117859]
 [ 142.98864746]
 [ 101.70191956]
 [ 145.31900024]
 [ 103.79642487]
 [ 170.0269165 ]
 [ 152.17144775]
 [ 141.85299683]
 [ 138.12550354]
 [ 192.3584137 ]
 [ 163.20774841]
 [ 145.43692017]
 [ 186.11605835]
 [ 157.7011261 ]
 [ 173.2724762 ]
 [ 184.07800293]
 [ 164.53826904]
 [ 170.88574219]
 [ 171.83169556]
 [ 163.77944946]
 [ 162.75912476]
 [ 193.57867432]]
STEP = 001000, cost = 4.6e+01, 예측값 = [[ 155.79348755]
 [ 185.46012878]
 [ 183.79823303]
 [ 197.92881775]
 [ 142.94723511]
 [ 101.91647339]
 [ 145.47525024]
 [ 104.10523224]
 [ 170.27351379]
 [ 152.73246765]
 [ 141.92948914]
 [ 138.35954285]
 [ 192.1013031 ]
 [ 162.80830383]
 [ 145.64486694]
 [ 186.24963379]
 [ 157.22314453]
 [ 173.49409485]
 [ 183.77397156]
 [ 164.26617432]
 [ 171.05285645]
 [ 171.97366333]
 [ 163.87850952]
 [ 162.25094604]
 [ 193.49662781]]
STEP = 001100, cost = 4.3e+01, 예측값 = [[ 155.62272644]
 [ 185.47862244]
 [ 183.69007874]
 [ 197.94621277]
 [ 142.90541077]
 [ 102.1204071 ]
 [ 145.62657166]
 [ 104.40414429]
 [ 170.50788879]
 [ 153.26844788]
 [ 142.00312805]
 [ 138.5827179 ]
 [ 191.85491943]
 [ 162.42503357]
 [ 145.84529114]
 [ 186.37664795]
 [ 156.76332092]
 [ 173.70927429]
 [ 183.48313904]
 [ 164.00630188]
 [ 171.21430969]
 [ 172.10874939]
 [ 163.97494507]
 [ 161.76498413]
 [ 193.41691589]]
STEP = 001200, cost = 4e+01, 예측값 = [[ 155.46055603]
 [ 185.49481201]
 [ 183.58660889]
 [ 197.96324158]
 [ 142.8631897 ]
 [ 102.31417084]
 [ 145.77307129]
 [ 104.69348145]
 [ 170.7305603 ]
 [ 153.78036499]
 [ 142.07395935]
 [ 138.79547119]
 [ 191.6187439 ]
 [ 162.05717468]
 [ 146.0383606 ]
 [ 186.49729919]
 [ 156.32089233]
 [ 173.91812134]
 [ 183.20481873]
 [ 163.75796509]
 [ 171.37023926]
 [ 172.23716736]
 [ 164.06867981]
 [ 161.3001709 ]
 [ 193.33934021]]
STEP = 001300, cost = 3.8e+01, 예측값 = [[ 155.30664062]
 [ 185.50897217]
 [ 183.48768616]
 [ 197.9800415 ]
 [ 142.82073975]
 [ 102.49828339]
 [ 145.91497803]
 [ 104.97361755]
 [ 170.94210815]
 [ 154.26937866]
 [ 142.14213562]
 [ 138.99832153]
 [ 191.39239502]
 [ 161.7041626 ]
 [ 146.22445679]
 [ 186.61195374]
 [ 155.8952179 ]
 [ 174.12097168]
 [ 182.9385376 ]
 [ 163.52081299]
 [ 171.52090454]
 [ 172.35928345]
 [ 164.15995789]
 [ 160.85568237]
 [ 193.26399231]]
STEP = 001400, cost = 3.6e+01, 예측값 = [[ 155.16055298]
 [ 185.52110291]
 [ 183.39309692]
 [ 197.99653625]
 [ 142.77804565]
 [ 102.67317963]
 [ 146.0524292 ]
 [ 105.2448349 ]
 [ 171.14305115]
 [ 154.73649597]
 [ 142.20776367]
 [ 139.19171143]
 [ 191.17546082]
 [ 161.3653717 ]
 [ 146.40379333]
 [ 186.72090149]
 [ 155.48564148]
 [ 174.31794739]
 [ 182.68380737]
 [ 163.29426575]
 [ 171.66648865]
 [ 172.47540283]
 [ 164.24874878]
 [ 160.43058777]
 [ 193.19070435]]
STEP = 001500, cost = 3.3e+01, 예측값 = [[ 155.02191162]
 [ 185.53137207]
 [ 183.30264282]
 [ 198.01274109]
 [ 142.73519897]
 [ 102.8392868 ]
 [ 146.18556213]
 [ 105.50745392]
 [ 171.3338623 ]
 [ 155.18266296]
 [ 142.27093506]
 [ 139.37605286]
 [ 190.96749878]
 [ 161.04016113]
 [ 146.5766449 ]
 [ 186.82435608]
 [ 155.09146118]
 [ 174.50920105]
 [ 182.44006348]
 [ 163.0778656 ]
 [ 171.80715942]
 [ 172.58575439]
 [ 164.3351593 ]
 [ 160.02403259]
 [ 193.11946106]]
STEP = 001600, cost = 3.1e+01, 예측값 = [[ 154.89038086]
 [ 185.53990173]
 [ 183.21614075]
 [ 198.02865601]
 [ 142.69224548]
 [ 102.99702454]
 [ 146.31452942]
 [ 105.76177216]
 [ 171.51502991]
 [ 155.60881042]
 [ 142.33174133]
 [ 139.55175781]
 [ 190.76817322]
 [ 160.72802734]
 [ 146.74327087]
 [ 186.92260742]
 [ 154.71209717]
 [ 174.69496155]
 [ 182.2068634 ]
 [ 162.8711853 ]
 [ 171.94313049]
 [ 172.69062805]
 [ 164.41925049]
 [ 159.63523865]
 [ 193.05018616]]
STEP = 001700, cost = 2.9e+01, 예측값 = [[ 154.76565552]
 [ 185.54676819]
 [ 183.13346863]
 [ 198.04428101]
 [ 142.64924622]
 [ 103.14676666]
 [ 146.43946838]
 [ 106.00806427]
 [ 171.68702698]
 [ 156.01580811]
 [ 142.39027405]
 [ 139.71922302]
 [ 190.57711792]
 [ 160.4283905 ]
 [ 146.90393066]
 [ 187.01591492]
 [ 154.34698486]
 [ 174.87536621]
 [ 181.98373413]
 [ 162.67378235]
 [ 172.07453918]
 [ 172.79029846]
 [ 164.50109863]
 [ 159.26341248]
 [ 192.98280334]]
STEP = 001800, cost = 2.8e+01, 예측값 = [[ 154.64735413]
 [ 185.55213928]
 [ 183.05438232]
 [ 198.05966187]
 [ 142.60624695]
 [ 103.28892517]
 [ 146.56053162]
 [ 106.24662018]
 [ 171.8502655 ]
 [ 156.40454102]
 [ 142.44665527]
 [ 139.87882996]
 [ 190.39398193]
 [ 160.14077759]
 [ 147.05882263]
 [ 187.10449219]
 [ 153.99554443]
 [ 175.0506134 ]
 [ 181.77027893]
 [ 162.48524475]
 [ 172.20155334]
 [ 172.88504028]
 [ 164.58074951]
 [ 158.90783691]
 [ 192.91732788]]
STEP = 001900, cost = 2.6e+01, 예측값 = [[ 154.53521729]
 [ 185.55604553]
 [ 182.97874451]
 [ 198.07472229]
 [ 142.56329346]
 [ 103.42381287]
 [ 146.67782593]
 [ 106.47769165]
 [ 172.00514221]
 [ 156.77580261]
 [ 142.50093079]
 [ 140.03089905]
 [ 190.21838379]
 [ 159.86463928]
 [ 147.2081604 ]
 [ 187.1885376 ]
 [ 153.65722656]
 [ 175.2208252 ]
 [ 181.56602478]
 [ 162.30516052]
 [ 172.32432556]
 [ 172.97499084]
 [ 164.65826416]
 [ 158.56776428]
 [ 192.85362244]]
STEP = 002000, cost = 2.5e+01, 예측값 = [[ 154.42892456]
 [ 185.55859375]
 [ 182.90646362]
 [ 198.08952332]
 [ 142.52043152]
 [ 103.55178833]
 [ 146.79150391]
 [ 106.70152283]
 [ 172.15206909]
 [ 157.13037109]
 [ 142.55319214]
 [ 140.17581177]
 [ 190.05004883]
 [ 159.59951782]
 [ 147.35217285]
 [ 187.26829529]
 [ 153.33151245]
 [ 175.38618469]
 [ 181.37059021]
 [ 162.13319397]
 [ 172.4430542 ]
 [ 173.06040955]
 [ 164.73371887]
 [ 158.24256897]
 [ 192.79165649]]
예상 점수는 [[ 181.73277283]]점입니다.
예상 점수는 [[ 145.86265564]
 [ 187.23129272]]입니다.

데이터가 많은 경우 Queue Runners를 이용하기

• 데이터가 많은 경우에 메모리에 한번에 올리기가 어려울 수 있기에 데이터를 조금씩 불러와 처리하는 방법

1. 여러 개의 파일을 읽어와 Filename Queue에 올린다.
2. Reader로 데이터를 읽는다.
3. 읽은 데이터를 Decoder로 변환한다.
4. 변환된 데이터를 Example Queue에 쌓는다.
5. 학습을 시킬 때, 필요한(batch) 만큼만 불러와 학습을 시킨다.

• 전체 과정을 TensorFlow가 알아서 관리를 해준다.
  

• 위의 그림을 수행하는 코드
  

import tensorflow as tf
tf.set_random_seed(777) # 실행할 때마다 같은 값이 나오도록 난수 발생의 초기값 설정

# 파일을 불러와 queue에 올리기
filename_queue = tf.train.string_input_producer(
    ['data-01-test-score.csv'], shuffle=False, name='filename_queue')

# reader로 데이터 읽기
reader = tf.TextLineReader()
key, value = reader.read(filename_queue)

# csv 데이터를 디코딩해서 queue에 올려놓기
record_defaults = [[0.], [0.], [0.], [0.]]
xy = tf.decode_csv(value, record_defaults=record_defaults)

# queue에서 일정부분(batch)씩 데이터 가져오기
train_x_batch, train_y_batch = tf.train.batch([xy[0:-1], xy[-1:]], batch_size=10)

X = tf.placeholder(tf.float32, shape=[None, 3])
Y = tf.placeholder(tf.float32, shape=[None, 1])

W = tf.Variable(tf.random_normal([3, 1]), name='weight')
b = tf.Variable(tf.random_normal([1]), name='bias')


# 가설식
hypothesis = tf.matmul(X, W) + b

# cost(loss) 함수
cost = tf.reduce_mean(tf.square(hypothesis - Y))

# 경사 하강법으로 학습
optimizer = tf.train.GradientDescentOptimizer(learning_rate=1e-5)
train = optimizer.minimize(cost)

# 세션에서 그래프 생성
sess = tf.Session()
# 그래프의 모든 변수 초기화
sess.run(tf.global_variables_initializer())

# filename queue 동작시키기
coord = tf.train.Coordinator()
threads = tf.train.start_queue_runners(sess=sess, coord=coord)

for step in range(2001):
    x_batch, y_batch = sess.run([train_x_batch, train_y_batch])
    cost_val, hy_val, _ = sess.run([cost, hypothesis, train],
                                   feed_dict={X: x_batch, Y: y_batch})

    if step % 100 == 0:
        print(f"STEP = {step:06}, cost = {cost_val:>02.2}, 예측값 = {hy_val}")

coord.request_stop()
coord.join(threads)


# 점수 에측을 해보자.
# 예상 점수는 185.34점
print(f"예상 점수는 {sess.run(hypothesis, feed_dict={X: [[100, 70, 101]]})}점 입니다.")
# 예상 점수는 [178.36, 17.04]점
print(f"다른 점수를 예상해보면 {sess.run(hypothesis, feed_dict={X: [[60, 70, 110], [90, 100, 80]]})}점 입니다.")

coord.request_stop()
coord.join(threads)

• 실행 결과
  

STEP = 000000, cost = 7.1e+03, 예측값 = [[ 235.2278595 ]
 [ 282.40145874]
 [ 278.3961792 ]
 [ 303.915802  ]
 [ 214.6239624 ]
 [ 159.15426636]
 [ 228.53509521]
 [ 170.92645264]
 [ 264.6505127 ]
 [ 246.59117126]]
STEP = 000100, cost = 4.6, 예측값 = [[ 154.07789612]
 [ 184.91040039]
 [ 182.31237793]
 [ 199.29498291]
 [ 140.26403809]
 [ 104.37033844]
 [ 150.24282837]
 [ 112.91205597]
 [ 173.57489014]
 [ 162.28497314]]
STEP = 000200, cost = 4.5, 예측값 = [[ 154.04267883]
 [ 184.92453003]
 [ 182.29525757]
 [ 199.30024719]
 [ 140.26908875]
 [ 104.4174881 ]
 [ 150.26643372]
 [ 112.95542145]
 [ 173.63035583]
 [ 162.39421082]]
STEP = 000300, cost = 4.5, 예측값 = [[ 154.00915527]
 [ 184.93783569]
 [ 182.27888489]
 [ 199.30531311]
 [ 140.27363586]
 [ 104.46237946]
 [ 150.28919983]
 [ 112.9972229 ]
 [ 173.68315125]
 [ 162.49847412]]
STEP = 000400, cost = 4.4, 예측값 = [[ 153.97727966]
 [ 184.95040894]
 [ 182.26325989]
 [ 199.31021118]
 [ 140.27775574]
 [ 104.50511169]
 [ 150.31112671]
 [ 113.03752899]
 [ 173.73344421]
 [ 162.5980072 ]]
STEP = 000500, cost = 4.4, 예측값 = [[ 153.94692993]
 [ 184.96224976]
 [ 182.24832153]
 [ 199.31491089]
 [ 140.28144836]
 [ 104.54580688]
 [ 150.33224487]
 [ 113.07639313]
 [ 173.78132629]
 [ 162.69300842]]
STEP = 000600, cost = 4.4, 예측값 = [[ 153.91807556]
 [ 184.97341919]
 [ 182.23405457]
 [ 199.31947327]
 [ 140.28475952]
 [ 104.58454895]
 [ 150.35263062]
 [ 113.11388397]
 [ 173.82691956]
 [ 162.78370667]]
STEP = 000700, cost = 4.3, 예측값 = [[ 153.89060974]
 [ 184.9839325 ]
 [ 182.22041321]
 [ 199.3238678 ]
 [ 140.28768921]
 [ 104.62140656]
 [ 150.37226868]
 [ 113.15003204]
 [ 173.87030029]
 [ 162.87026978]]
STEP = 000800, cost = 4.3, 예측값 = [[ 153.86450195]
 [ 184.99382019]
 [ 182.20739746]
 [ 199.32810974]
 [ 140.29025269]
 [ 104.65649414]
 [ 150.39120483]
 [ 113.18490601]
 [ 173.91160583]
 [ 162.95289612]]
STEP = 000900, cost = 4.3, 예측값 = [[ 153.83964539]
 [ 185.00311279]
 [ 182.19496155]
 [ 199.33216858]
 [ 140.29249573]
 [ 104.68988037]
 [ 150.4094696 ]
 [ 113.21853638]
 [ 173.95091248]
 [ 163.03175354]]
STEP = 001000, cost = 4.3, 예측값 = [[ 153.81602478]
 [ 185.0118866 ]
 [ 182.18305969]
 [ 199.33612061]
 [ 140.29444885]
 [ 104.7216568 ]
 [ 150.42707825]
 [ 113.25099945]
 [ 173.98832703]
 [ 163.10702515]]
STEP = 001100, cost = 4.3, 예측값 = [[ 153.79354858]
 [ 185.02008057]
 [ 182.17169189]
 [ 199.33990479]
 [ 140.29608154]
 [ 104.75189972]
 [ 150.44403076]
 [ 113.28232574]
 [ 174.02389526]
 [ 163.17886353]]
STEP = 001200, cost = 4.3, 예측값 = [[ 153.7722168 ]
 [ 185.02780151]
 [ 182.16082764]
 [ 199.34359741]
 [ 140.29745483]
 [ 104.78065491]
 [ 150.4604187 ]
 [ 113.31253052]
 [ 174.05776978]
 [ 163.24742126]]
STEP = 001300, cost = 4.3, 예측값 = [[ 153.75189209]
 [ 185.03504944]
 [ 182.15046692]
 [ 199.34712219]
 [ 140.29856873]
 [ 104.80802155]
 [ 150.47621155]
 [ 113.34170532]
 [ 174.08998108]
 [ 163.31285095]]
STEP = 001400, cost = 4.2, 예측값 = [[ 153.73258972]
 [ 185.04185486]
 [ 182.14054871]
 [ 199.35054016]
 [ 140.29945374]
 [ 104.83404541]
 [ 150.49145508]
 [ 113.36985016]
 [ 174.12062073]
 [ 163.37532043]]
STEP = 001500, cost = 4.2, 예측값 = [[ 153.71424866]
 [ 185.04821777]
 [ 182.131073  ]
 [ 199.35385132]
 [ 140.30010986]
 [ 104.85879517]
 [ 150.50616455]
 [ 113.39702606]
 [ 174.14978027]
 [ 163.43490601]]
STEP = 001600, cost = 4.2, 예측값 = [[ 153.69680786]
 [ 185.05418396]
 [ 182.12202454]
 [ 199.35704041]
 [ 140.30055237]
 [ 104.88233948]
 [ 150.52033997]
 [ 113.42326355]
 [ 174.17750549]
 [ 163.49179077]]
STEP = 001700, cost = 4.2, 예측값 = [[ 153.68023682]
 [ 185.05975342]
 [ 182.1133728 ]
 [ 199.36010742]
 [ 140.30078125]
 [ 104.90473175]
 [ 150.5340271 ]
 [ 113.44860077]
 [ 174.20388794]
 [ 163.54608154]]
STEP = 001800, cost = 4.2, 예측값 = [[ 153.664505  ]
 [ 185.06495667]
 [ 182.10508728]
 [ 199.36308289]
 [ 140.30085754]
 [ 104.9260025 ]
 [ 150.54724121]
 [ 113.47304535]
 [ 174.22892761]
 [ 163.59788513]]
STEP = 001900, cost = 4.2, 예측값 = [[ 153.64956665]
 [ 185.06985474]
 [ 182.09719849]
 [ 199.36595154]
 [ 140.30075073]
 [ 104.94623566]
 [ 150.55999756]
 [ 113.49666595]
 [ 174.2527771 ]
 [ 163.64732361]]
STEP = 002000, cost = 4.2, 예측값 = [[ 153.63536072]
 [ 185.0743866 ]
 [ 182.08964539]
 [ 199.36869812]
 [ 140.30047607]
 [ 104.96544647]
 [ 150.5723114 ]
 [ 113.51947784]
 [ 174.27540588]
 [ 163.69447327]]
예상 점수는 [[ 185.33529663]]점 입니다.
다른 점수를 예상해보면 [[ 178.36242676]
 [ 177.03689575]]점 입니다.

다변수 선형 회귀(Multi-variable Linear Regression)

변수가 하나일 때 선형 회귀에 사용했던 방법

• Hypothesis :
  

\begin{equation} H(x) = W\times x + b \tag{1}\end{equation}

• cost(loss) 함수 : 가설 식 (1)과 실제 값과의 차이
  

\begin{eqnarray} \textrm{cost(loss)}(W,b) &=& \frac{1}{m}\sum_{i=1}^m\Big(H(x_i)-y_i\Big)^2\\ &=& \frac{1}{m}\sum_{i=1}^m\Big( \big(W\times x_i + b\big) -y_i \Big)^2 \tag{2}\end{eqnarray}

• Gradient Descent Algorithm : cost(loss) 함수가 극소가 되는 값을 구하는 방법
  

\begin{equation} W = W - \alpha \times \frac{\partial}{\partial W}\textrm{cost(loss)}(W,b) \tag{3}\end{equation}

변수가 3개일 때의 선형 회귀식

• 다음과 같이 3개의 입력값에 대한 결과값이 있을 때 선형 회귀식을 구하는 방법을 생각해본다.
• 인스턴스(instance) : 실제 각각의 데이터
• 아래 표에서는 5개의 인스턴스를 사용해 가설을 만들게 된다.
  

• 가설(hypothesis) : 인스턴스가 1개일 때, 변수는 3개이기 때문에 단변수일 때의 가설 식 (1)을 다음 식 (4)처럼 쓸 수 있다.

\begin{eqnarray} H(x_1, x_2, x_3) = w_1\times x_1 + w_2\times x_2 + w_3\times x_3 + b\tag{4} \end{eqnarray}

• cost(loss) 함수 : 위 식 (2)는 다음 식 (5)처럼 쓸 수 있다.

\begin{eqnarray}\textrm{cost(loss)}(W,b) = \frac{1}{m} \sum_{i=1}^m\Big(H(x_{1_i},x_{2_i},x_{3_i}) - y_i\Big)^2\tag{5}\end{eqnarray}

변수가 $n$개일 때로 일반화한 선형 회귀식

• 가설(hypothesis) : 인스턴스가 1개에 대하여 변수가 \(n\)개일 때의 가설은 식 (6)처럼 쓸 수 있다

\begin{eqnarray} H(x_1, x_2,\ldots,x_n) = w_1\cdot x_1 + w_2\cdot x_2 +\cdots + w_n\cdot x_n + b\tag{6} \end{eqnarray}

• 다변수일 때의 식은 항이 여러 개로 나와 길게 쓰는 것이 불편하기 때문에 식 (6)은 행렬식을 이용하여 식 (7)처럼 쓸 수 있다.

• 데이터 \(x_i\)의 값들이 주어지기 때문에 계수로 쓰고, \(w_i\)는 우리가 예측해야 하는 값이기 때문에 변수로 표기해 식을 정리한다.
  

\begin{eqnarray} H(x_1, x_2,\ldots,x_n) &=& w_1\cdot x_1 + w_2\cdot x_2 +\cdots + w_n\cdot x_n + b\\&=& x_1\cdot w_1 + x_2\cdot w_2 +\cdots + x_n\cdot w_n + b\\&=&(x_1,x_2,\ldots, x_n)\cdot\left( \begin{array}{c} w_1\\ w_2\\ \vdots\\ w_n\end{array} \right) + b\tag{7} \end{eqnarray}

• 위의 변수들을 행렬로 해서 정리하면 다음과 같이 간단히 정리할 수 있다.

• \(\mathbf{X}=[x_1,x_2,x_3,\ldots,x_n]\)
• \(\mathbf{W}=[w_1,w_2,w_3,\ldots,w_n]\)

\begin{eqnarray}H(\mathbf{X}) = \mathbf{X}\times \mathbf{W}^T+b\tag{8}\end{eqnarray}

행렬식을 사용하는 가설식

• 아래 시험성적표에 대한 가설식을 만들어 보자.

• 변수가 3개이기 때문에 가설은 식 (9)처럼 쓸 수 있다.
  

\begin{eqnarray} H(x_1, x_2,x_3) &=& x_1\times w_1 + x_2\times w_2 + x_e\times w_3 + b\\&=&(x_1,x_2,x_3)\left(\begin{array}{c}w_1\\w_2\\w_3\end{array}\right)+b\\&=&\mathbf{X}\mathbf{W}^T + b=H(\mathbf{X})\tag{9}\end{eqnarray}

• 우리의 예에서는 인스턴스가 5개이기 때문에 가설은 식(10)처럼 쓸 수 있다.

\begin{eqnarray}\left( \begin{array}{c} x_{1_1} w_1 + x_{1_2} w_2 + x_{1_3} w_3 + b_1\\ x_{2_1} w_1 + x_{2_2} w_2 + x_{2_3} w_3 + b_2\\ x_{3_1} w_1 + x_{3_2} w_2 + x_{3_3} w_3 + b_3\\x_{4_1} w_1 + x_{4_2} w_2 + x_{4_3} w_3 + b_4\\ x_{5_1} w_1 + x_{5_2} w_2 + x_{5_3} w_3 + b_5\end{array} \right) &=&\left( \begin{array}{ccc}x_{1_1} & x_{1_2} & x_{1_3}\\ x_{2_1} & x_{2_2} & x_{2_3}\\ x_{3_1} & x_{3_2} & x_{3_3}\\ x_{4_1} & x_{4_2} & x_{4_3}\\x_{5_1} & x_{5_2} & x_{5_3}\end{array}\right)\cdot\left( \begin{array}{c}w_1\\ w_2\\ w_3\end{array} \right)+\left( \begin{array}{c}b_1\\b_2\\b_3\\b_4\\b_5\end{array} \right)\tag{10}\\ &=&\mathbf{X}\cdot\mathbf{W}+\mathbf{B}\\ &=& H(\mathbf{X})\end{eqnarray}

• 식 (10)을 차원(dimension)(텐서플로우의 데이터 모양(shape))으로 표현하면 다음과 같다.

• instance \(\mathbf{X}\) 행렬의 차원은 $[5,3]$
• weight \(\mathbf{W}\) 행렬의 차원은 $[3,1]$
• bias \(\mathbf{B}\) 행렬의 차원은 $[5,1]$
  

$$[5,1]=[5,3] \times [3,1] + [5,1]$$

결과값이 2개인 경우의 가설식

• 결과값이 여러 개인 경우도 고려해볼 수가 있는데 2개의 경우에 몇 차원의 weight 행렬식을 사용해야할까?

• 식 (11)과 같이 \([3,2]\) 차원의 행렬식 weight를 사용하면 된다.
  

\begin{eqnarray}\begin{array}{lcl}[5, 3] \times [?, ?] &=& [?, 2]\\ [5,3] \times [3, 2]&=&[5,2]\end{array}\tag{11}\end{eqnarray}

\begin{eqnarray}\left( \begin{array}{cc} x_{1_1} w_{1_1} + x_{1_2} w_{2_1} + x_{1_3} w_{3_1} + b_1&x_{1_1} w_{1_2} + x_{1_2} w_{2_2} + x_{1_3} w_{3_2} + b_2\\ x_{2_1} w_{1_1} + x_{2_2} w_{2_1} + x_{2_3} w_{3_1} + b_1&x_{2_1} w_{1_2} + x_{2_2} w_{2_2} + x_{2_3} w_{3_2} + b_2\\ x_{3_1} w_{1_1} + x_{2_2} w_{2_1} + x_{3_3} w_{3_1} + b_1&x_{3_1} w_{1_2} + x_{3_2} w_{2_2} + x_{3_3} w_{3_2} + b_2\\x_{4_1} w_{1_1} + x_{4_2} w_{2_1} + x_{4_3} w_{3_1} + b_1&x_{4_1} w_{1_2} + x_{4_2} w_{2_2} + x_{4_3} w_{3_2} + b_2\\ x_{5_1} w_{1_1} + x_{5_2} w_{2_1} + x_{5_3} w_{3_1} + b_1&x_{5_1} w_{1_2} + x_{5_2} w_{2_2} + x_{5_3} w_{3_2} + b_2\end{array} \right) &=&\left( \begin{array}{ccc}x_{1_1} & x_{1_2} & x_{1_3}\\ x_{2_1} & x_{2_2} & x_{2_3}\\ x_{3_1} & x_{3_2} & x_{3_3}\\ x_{4_1} & x_{4_2} & x_{4_3}\\x_{5_1} & x_{5_2} & x_{5_3}\end{array}\right)\cdot\left( \begin{array}{cc}w_{1_1} & w_{1_2}\\ w_{2_1} & w_{2_2}\\ w_{3_1} & w_{3_2}\end{array} \right)+\left( \begin{array}{cc}b_{1_1} & b_{1_2}\\b_{2_1} & b_{2_2}\\b_{3_1} & b_{3_2}\\b_{4_1} & b_{4_2}\\b_{5_1} & b_{5_2}\end{array} \right)\end{eqnarray}

결론 : 행렬식을 사용하면 많은 인스턴스 및 다변수의 경우에도 쉽게 수식으로 정리, 표현할 수 있다.

• 이론으로 가설식을 다룰 때에는 weight \(w\)를 계수로 하고 변수 \(x\)의 순서로 쓰지만, 실제에서는 weight와 변수의 순서를 바꾸면 행렬식을 그대로 쓸 수 있게 코딩으로 바로 구현하는 것이 쉽다.
  

• 이론 가설식(theory hypothesis) : \(H(\mathbf{X}) = \mathbf{W}\times \mathbf{X}+\mathbf{B}\)

• 구현 가설식(implementation hypothesis) : \(H(\mathbf{X}) = \mathbf{X}\times \mathbf{W}^T+\mathbf{B}\)

텐서플로우의 변수

변수의 생성

• 텐서와 연산(Op) 객체는 변경할 수 없다. 그러나 기계 학습의 속성 상 시간에 따라 변경되는 값을 저장할 수 있는 방법이 필요

• 텐서플로우에서는 sess.run()을 여러 번 호출하는 동안 값을 유지하면서 변경하기 위해 변수(variable) 객체를 사용

• tf.Variable() 생성자를 사용하여 변수 객체를 생성

import tensorflow as tf

my_var = tf.Variable(3, name="my_variable")

• 변수는 텐서를 사용할 수 있는 어떤 텐서플로우 함수/연산에서도 사용 가능

• 변수의 현재값은 변수를 사용하는 연산에 전달

add = tf.add(5, my_var)
mul = tf.multiply(8, my_var)

• 변수의 초기값은 보통 많은 0이나 1 또는 난수들로 이루어진 큰 텐서들(large tensors)이다.
• 이런 일반적으로 많이 사용되는 값들을 만들기 쉽게 다양한 연산이 존재
• tf.zero() : 영으로 이루어진 텐서
• tf.ones() : 1로 이루어진 텐서
• tf.random_normal() : 정규분포를 따르는 난수들로 이루어진 텐서
• tf.random_uniform() : 난수로 균등하게 이루어진 텐서
  

# 2x2 영 행렬
zeros = tf.zeros([2, 2])

# 길이가 6인 1로 이루어진 벡터
ones = tf.ones([6])

# 평균이 0이고 표준편차가 2인 정규 분포를 따르는 난수로 이루어진 3x3x3 텐서
normal = tf.random_normal([3, 3, 3], mean=0.0, stddev=2.0)

# 0과 10 사이 난수로 균등하게 이루어진  3x3x3 텐서
uniform = tf.random_uniform([3, 3, 3], minval=0, maxval=10)

• tf.truncated_normal() : 평균에서 표준편차 이상의 값은 생성하지 않기 때문에 텐서 내부의 1~2개의 값이 다른 값들과 많은 차이가 날 가능성을 방지해준다.

# trunc 텐서에는 3이하나 7이상의 값이 없다.
trunc = tf.truncated_normal([2, 2], mean=5.0, stddev=1.0)

• 위와 같은 연산은 텐서를 만들 때 변수의 초기값을 전달할 수 있다.

# 평균이 0이고 표준편차가 1인 정규분포를 따르는 난수로 이루어진 2x2 행렬
random_var = tf.Variable(tf.truncated_normal([2, 2]))

변수의 초기화

• 변수 객체는 다른 텐서플로우의 다른 객체들처럼 그래프 내부에 존재
  

• 변수의 상태는 Session()에 의해 관리됨

• 변수를 사용하기 위해서는 세션 내부에서 변수들을 초기화해야 한다!

• 초기화가 이루어지면 Session()이 변수의 현재 값들을 추적

• 초기화 : tf.global_variables_initializer() 연산을 사용하여 sess.run()에 전달

init = tf.global_variables_initializer()

sess = tf.Session()
sess.run(init)

• 그래프에서 정의된 변수들의 일부분(subset)만 초기화하려면 tf.variables_initializer=()를 사용

• 초기화될 변수들의 리스트를 받아들임

var1 = tf.Variable(0, name="initialize_me")
var2 = tf.Variable(1, name="no_initialization")

init = tf.variables_initializer([var1], name="init_var1")

sess = tf.Session()
sess.run(init)

변수값 변경하기

• 변수값을 변경하기 위해서는 변수.assign() 메서드를 사용
  

• 변수.assign()은 연산이기 때문에 세션에서 실행되어야 효과가 발생

import tensorflow as tf

# 변수에 값 1을 할당
my_var = tf.Variable(1)

# 연산이 실행될 때마다 변수에 2를 곱하는 연산
my_var_times_two = my_var.assign(my_var * 2)

# 연산 초기화
init = tf.global_variables_initializer()

# 세션 시작
sess = tf.Session()

# 변수 초기화
sess.run(init)

# 변수에 2를 곱한 결과 2를 반환
sess.run(my_var_times_two)

# 변수에 2를 곱한 결과 4를 반환
sess.run(my_var_times_two)

# 변수에 2를 곱한 결과 8을 반환
sess.run(my_var_times_two)

• 세션을 통해 위의 코드를 실행한 결과
  

# 위의 코드를 다음과 같이 실행
print(f"1번째 세션 실행 결과 = {sess.run(my_var_times_two)}")
print(f"2번째 세션 실행 결과 = {sess.run(my_var_times_two)}")
print(f"3번째 세션 실행 결과 = {sess.run(my_var_times_two)}")

# 결과는 예상대로 다음과 같다.
1번째 세션 실행 결과 = 2
2번째 세션 실행 결과 = 4
3번째 세션 실행 결과 = 8

• 변수값의 증가 :  변수.assign_add() 메서드를 사용
  

• 변수값의 감소 :  변수.assign_sub() 메서드를 사용

# 변수에 값 1을 증가시킴
sess.run(my_var.assign_add(1))

# 변수에 값 1을 감소시킴
sess.run(my_var.assign_sub(1))

• 앞의 코드에서 변수의 값을 증감하여 실행한 결과
  

import tensorflow as tf

my_var = tf.Variable(1)
my_var_times_two = my_var.assign(my_var * 2)

init = tf.global_variables_initializer()
sess = tf.Session()
sess.run(init)

print(f"1번째 세션 실행 결과 = {sess.run(my_var_times_two)}")
print(f"2번째 세션 실행 결과 = {sess.run(my_var_times_two)}")

# 변수에 값 1을 증가시킴
print(f"1을 증가시킨 my_var = {sess.run(my_var.assign_add(1))}")
print(f"1을 증가시킨 후 1번째 세션 실행 결과 = {sess.run(my_var_times_two)}")
print(f"1을 증가시킨 후 2번째 세션 실행 결과 = {sess.run(my_var_times_two)}")

# 변수에 값 1을 감소시킴
print(f"1을 감소시킨 my_var = {sess.run(my_var.assign_sub(1))}")
print(f"1을 감소시킨 후 1번째 세션 실행 결과 = {sess.run(my_var_times_two)}")
print(f"1을 감소시킨 후 2번째 세션 실행 결과 = {sess.run(my_var_times_two)}")

# 실행 결과
1번째 세션 실행 결과 = 2
2번째 세션 실행 결과 = 4
1을 증가시킨 my_var = 5
1을 증가시킨 후 1번째 세션 실행 결과 = 10
1을 증가시킨 후 2번째 세션 실행 결과 = 20
1을 감소시킨 my_var = 19
1을 감소시킨 후 1번째 세션 실행 결과 = 38
1을 감소시킨 후 2번째 세션 실행 결과 = 76

세션에 따른 변수값의 변화

• 변수들은 세션에 따라 독립적으로 관리된다.
  

• 각 세션은 그래프에 정의된 변수들의 현재값을 가진다.

import tensorflow as tf

# 변수에 0을 할당하고 초기화
my_var = tf.Variable(0)
init = tf.variables_initializer([my_var])

# 2개의 세션을 만든다.
sess1 = tf.Session()
sess2 = tf.Session()

# 세션1에서 변수를 초기화하고 5를 증가시킨다.
sess1.run(init)
result1 = sess1.run(my_var.assign_add(5))
print(f"세션1 : 초기화 후 변수에 5 증가시킨 결과 = {result1:02}")

# 세션2에서 변수를 초기화하고 2를 증가시킨다.
sess2.run(init)
result2 = sess2.run(my_var.assign_add(2))
print(f"세션2 : 초기화 후 변수에 2 증가시킨 결과 = {result2:02}")

# 세션1에서 변수를 초기화하지않고 변수에 다시 5를 증가시킨다.
print(f"세션1에 다시 5를 증가시킨 결과 = {sess1.run(my_var.assign_add(5)):02}")

# 세션2에서 변수를 초기화하지않고 변수에 다시 2를 증가시킨다.
print(f"세션2에 다시 2를 증가시킨 결과 = {sess2.run(my_var.assign_add(2)):02}")

# 실행 결과
세션1 : 초기화 후 변수에 5 증가시킨 결과 = 05
세션2 : 초기화 후 변수에 2 증가시킨 결과 = 02
세션1에 다시 5를 증가시킨 결과 = 10
세션2에 다시 2를 증가시킨 결과 = 04

변수를 초기값으로 재설정하기

• 전체 변수 초기값으로 재설정 : tf.global_variables_initializer()를 다시 호출
  

• 변수의 일부분만 초기값으로 재설정 : tf.variables_initializer()를 다시 호출

import tensorflow as tf

# 변수에 0을 할당
my_var = tf.Variable(0)
init = tf.global_variables_initializer()

# 세션을 만들고 변수를 초기화
sess = tf.Session()
sess.run(init)

# 변수에 10을 증가시킴
result = sess.run(my_var.assign_add(10))
print(f"my_var 변수에 10을 증가시킨 결과 = {result}")

# 변수를 다시 초기화
sess.run(init)
print(f"초기화한 후의 my_var의 값= {sess.run(my_var)}")